Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специального вида правой частью

Метод неопределенных коэффициентов позволяет найти частное решение такого уравнения для следующих случаев.

Рассмотрим неоднородное ЛДУ второго порядка с постоянными коэффициентами

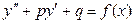. (11)

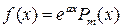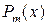1) Пусть правая часть уравнения имеет вид , где - многочлен степени .

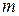а) Если число a не является корнем характеристического уравнения для уравнения (11)

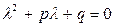, (12)

то частное решение неоднородного уравнения ищется в том же виде, что и правая часть уравнения, т.е.

,

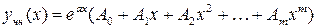где 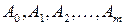- некоторые числа. Здесь и в дальнейшем для их нахождения нужно подставить 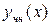в уравнение (11) и приравнять коэффициенты при одинаковых степенях х в обеих частях получившегося уравнения.

б) Пусть число a совпадает с корнем характеристического уравнения (12) кратности 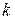(k =1 или 2). Тогда частное решение (11) ищется в том же виде, но с сомножителем 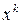, т.е.

.

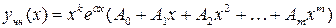И далее аналогично пункту а).

2) Пусть правая часть уравнения (11) есть

,

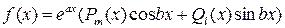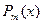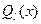где и - некоторые многочлены степеней m и l соответственно, .

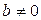а) Если комплексное число 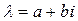не является корнем характеристического уравнения (12), тогда частное решение неоднородного уравнения ищется в виде

,

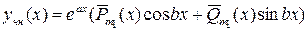где 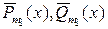- многочлены степени 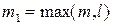с неопределенными коэффициентами.

б) Если 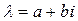является корнем характеристического уравнения (12), тогда частное решение неоднородного ЛДУ (11) ищется в виде

, .

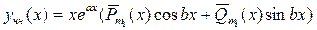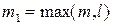СПИСОК ЛИТЕРАТУРЫ

1. Ефимов Н.В. Краткий курс аналитической геометрии. М.: Физматлит, 2002.

2. Шипачев В.С. Высшая математика. М.: Высшая школа, 2002.

3. Шипачев В.С. Сборник задач по высшей математике. М.: Высшая школа, 2002.

4. Пискунов Н.С. Сборник индивидуальных задач по высшей математике. Часть 1,2. М.: Высшая школа, 2002.

5. Рябушко А.П. Сборник индивидуальных задач по высшей математике. Минск: Высшая школа, 2002.-ч. 1,2,3.

6. Бугров Я.С., Никольский С.М. Высшая математика. Задачник. М.: Наука, 1982.

7. Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 1986.

8. Сборник задач по математике. Линейная алгебра и основы математического анализа. Под редакцией Ефимова А. В., Демидовича Б. П. М, 1981.

9. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре. М.: Наука, 1987.

10. Гусятников П. В., Резниченко С. В. Векторная алгебра в примерах и задачах. М.: Высшая школа, 1985.

11. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М.: Высшая школа, 1986.-ч. 1,2.

12. Крутицкая Н.Т., Шишков А.А. Линейная алгебра в вопросах и задачах. М.: Высшая школа, 1985г.

13. Головина Л.И. Линейная алгебра и некоторые ее приложения. М.: Наука, 1985.

14. Кузнецов Л.А. Сборник задач по высшей математике (типовые расчеты). М.: Высшая школа. 1983.

15. Краснов М.Л. Обыкновенные дифференциальные уравнения. М.: Наука. 1983.

СОДЕРЖАНИЕ

Глава I. Линейная алгебра 3

§1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства

определителей 3

§2. Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца 4

§3. Операции над матрицами 5

Date: 2015-04-23; view: 646; Нарушение авторских прав