Экстремумы функции нескольких переменных

4.1. Точка 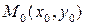называется точкой максимума функции 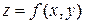, если существует окрестность 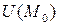такая, что для всех из этой окрестности выполняется неравенство

.

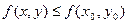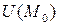Если для всех из окрестности выполняется неравенство

,

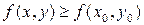то точка называется точкой минимума. Значение функции в точке максимума 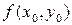, называется максимумом функции, а ее значение в точке минимума – минимумом. Точки максимума и минимума называются экстремальными точками функции, а максимумы и минимумы называются экстремумами функции (см. рис. 4).

Рис. 4

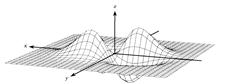
Пусть функция 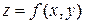определена в некоторой окрестности точки . Если в каждая частная производная 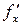и 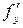равна нулю или не существует, то называется критической точкой функции .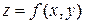

Теорема 1. (Необходимое условие экстремума). Если 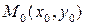является экстремальной точкой функции 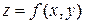, то – критическая точка этой функции.

Сформулируем необходимые условия экстремума для дифференцируемой функции n переменных .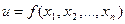

Если точка 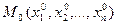является экстремальной точкой функции 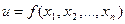, дифференцируемой в некоторой окрестности 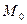, то 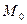- стационарная точка этой функции, то есть ее координаты удовлетворяют системе уравнений

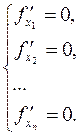
Теорема 2. (Достаточные условия экстремума). Пусть функция 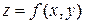трижды дифференцируема в некоторой окрестности своей критической точки 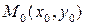. Обозначим 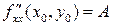, , 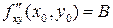, 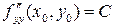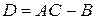. Тогда:

1) Если 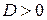, то точка экстремальная для функции 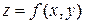, причем если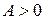 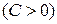, то это точка минимума, а если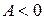 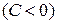, то точка - точка максимума.

2) Если 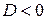, то в точке 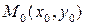экстремума нет.

Глава 6. НЕОПРЕДЕЛЕННЫЕ И ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ

Date: 2015-04-23; view: 626; Нарушение авторских прав