Линейные уравнения первого порядка. Определение.Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной вида

Определение.Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной вида

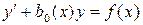, (1)

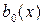где и 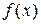- непрерывные функции от x.

Найдем решение уравнения (1) в виде произведения двух функций

.

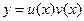Дифференцируя обе части этого равенства, находим

.

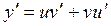Подставляя полученное значение производной 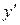в уравнение (1), получим

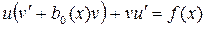. (2)

Выберем функцию 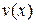так, чтобы

.

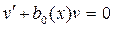Разделяя переменные в этом дифференциальном уравнении, находим

.

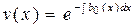Подставляя найденное значение 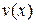в (2), получим

.

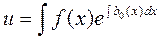
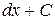Окончательно, общее решение уравнения (1) записывается в виде

.

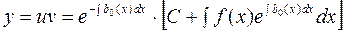Основные понятия об уравнениях высшего порядка

Если уравнение 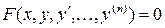удается разрешить относительно старшей производной, т.е. записать в виде

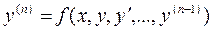, (1)

то такое уравнение называется уравнением, разрешенным относительно старшей производной.

Говорят, что решение уравнения второго порядка 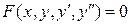удовлетворяет начальным условиям для заданных значений 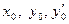, если

.

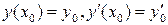Геометрически это значит, что соответствующая интегральная кривая уравнения проходит через точку 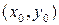плоскости Oxy и имеет в этой точке касательную с угловым коэффициентом .

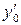Для уравнения n-го порядка (1) начальными условиями называют систему из n условий

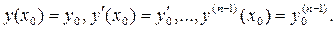(2)

Отыскание решения уравнения (1), удовлетворяющего заданным начальным условиям (2), называется решением задачи Коши для этого уравнения.

Теорема Коши. Если функция 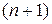-й переменной 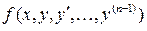непрерывна в некоторой области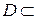 и имеет в ней непрерывные частные производные по 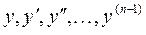, то какова бы ни была точка 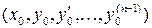из этой области, существует единственное решение 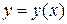уравнения 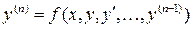, определенное в некотором интервале, содержащем точку 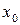и удовлетворяющее начальным условиям (2).

Определение. Функция 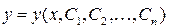, зависящая от n постоянных 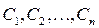, называется общим решением уравнения (1) в некоторой области 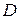плоскости Oxy, если она является решением этого уравнения для любых значений постоянных 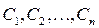и, если любое решение уравнения, лежащее в области 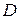, может быть записано в виде 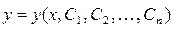для конкретных .

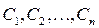Решения, получающиеся из общего при конкретных значениях постоянных 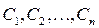, называются частными решениями данного уравнения. Неявно заданное общее или частное решения уравнения называются соответственно его общим и частным интегралами.

Date: 2015-04-23; view: 747; Нарушение авторских прав