
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод интегрирования по частям
|
|
Теорема 2. Пусть функции 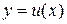 и
и 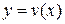 непрерывно дифференцируемы, тогда
непрерывно дифференцируемы, тогда
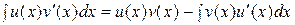 .
.
Последнюю формулу часто записывают в сокращенном виде
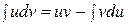 .
.
Этот метод применяется в случае, когда подынтегральная функция имеет вид произведения 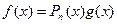 , где
, где 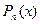 - многочлен, а
- многочлен, а 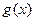 - тригонометрическая, показательная
- тригонометрическая, показательная 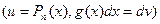 , обратная тригонометрическая, или логарифмическая функция
, обратная тригонометрическая, или логарифмическая функция 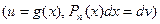 .
.
В заключение отметим, что класс функций, первообразные которых находятся в виде элементарных функций (говорят интегрируемых в квадратурах) довольно узок. Например, 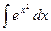 невозможно записать с помощью элементарной функции.
невозможно записать с помощью элементарной функции.
§3. Определенный интеграл как предел интегральных сумм
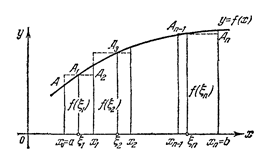 Криволинейной трапецией называется область на плоскости
Криволинейной трапецией называется область на плоскости 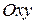 ограниченная осью
ограниченная осью 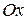 , прямыми
, прямыми 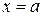 ,
,  где
где 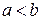 и графиком непрерывной на отрезке
и графиком непрерывной на отрезке  функции
функции  (см. рис.1).
(см. рис.1).
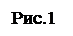 Разбиением отрезка
Разбиением отрезка  на n частей называется набор чисел
на n частей называется набор чисел 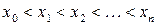 из этого отрезка, где
из этого отрезка, где  и
и 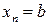 . В каждом отрезке (элементарном участке)
. В каждом отрезке (элементарном участке)  разбиения выберем некоторую точку
разбиения выберем некоторую точку 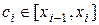 . Такое разбиение обозначим буквой
. Такое разбиение обозначим буквой  , а длину элементарного участка - через
, а длину элементарного участка - через 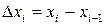 . Пусть на отрезке
. Пусть на отрезке  определена некоторая функция
определена некоторая функция  .
.
Определение.Интегральной суммой для функции  , построенной по разбиению
, построенной по разбиению  отрезка
отрезка  , называется сумма произведений значений функции в выбранных точках
, называется сумма произведений значений функции в выбранных точках  на длины элементарных участков.
на длины элементарных участков.
Обозначение:  . Если
. Если 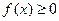 в
в  , то
, то 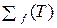 приближенно равна площади соответствующей криволинейной трапеции.
приближенно равна площади соответствующей криволинейной трапеции.
Определение.Определенным интегралом от функции  на отрезке
на отрезке  называется предел интегральных сумм этой функции по разбиениям отрезка
называется предел интегральных сумм этой функции по разбиениям отрезка  , у которых максимальный
, у которых максимальный 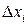 стремится к нулю, т.е.
стремится к нулю, т.е.
 .
.
Если 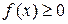 в
в  , то этот интеграл выражает точную площадь соответствующей криволинейной трапеции.
, то этот интеграл выражает точную площадь соответствующей криволинейной трапеции.
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке  или имеет на нем конечное число точек разрыва первого рода, то эта функция интегрируема на
или имеет на нем конечное число точек разрыва первого рода, то эта функция интегрируема на  , т.е.
, т.е. 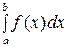 существует.
существует.
Date: 2015-04-23; view: 699; Нарушение авторских прав