Линейная независимость функций

Определение. Функции 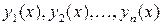определенные на интервале 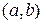называются линейно независимыми на этом интервале, если соотношение

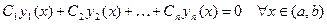(4)

выполняется только при всех 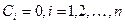(т.е. если это соотношение не выполняется для отличных от нуля чисел 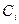). Система n функций называется линейно зависимой на 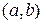, если существуют числа 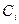, не все равные нулю, такие, что выполняется соотношение (4).

В частности, две функции 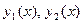являются линейно независимыми на интервале 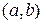только в том случае, когда их отношение 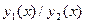- непостоянная функция на этом промежутке .

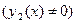6.4. Общее решение линейного однородного дифференциального уравнения n -го порядка

Рассмотрим однородное линейное дифференциальное уравнение

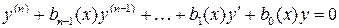, (5)

Если n частных решений однородного ЛДУ (5) линейно независимы, то эта система называется фундаментальной системой решений (ФСР) уравнения (5).

Теорема. Если - фундаментальная система решений уравнения (5), то функция

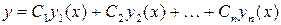(6)

является общим решением этого линейного дифференциального уравнения.

Date: 2015-04-23; view: 762; Нарушение авторских прав