Первообразная и неопределенный интеграл. Их свойства

Основные определения

Определение.Первообразной для функции , определенной в интервале 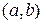, называется такая функция 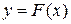, производная которой совпадает с 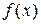в интервале 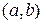, т.е.

.

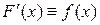
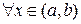Теорема 1. Есл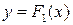и и 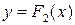две первообразные для функции в 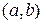, то найдется такое число C, что в .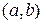

Из этой теоремы следует, что если есть одна первообразная 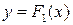функции , то любая другая ее первообразная имеет вид 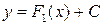для некоторого числа .

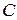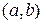Определение. Множество всех первообразных для функции на интервале называется ее неопределенным интегралом.

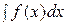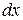Он обозначается символами , где знак интеграла, - дифференциал переменной x. Если 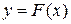- какая либо первообразная функции , то

, .

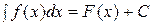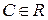Таблица основных неопределенных интегралов

Здесь u - независимая переменная или непрерывно дифференцируемая функция u=u(x).

1. , ;

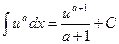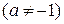2. ;

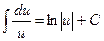3. 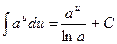, 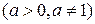. В частности, ;

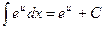4. ;

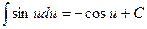5. ;

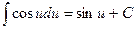6. ;

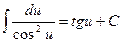7. ;

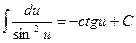8. ;

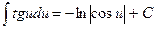9. ;

10. ;

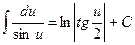11. ;

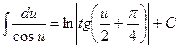12. , ;

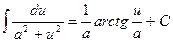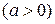13. , ;

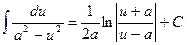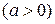14. , ;

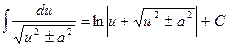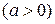15. , ;

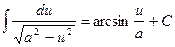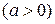16. ;

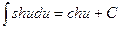17. ;

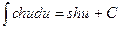18. ;

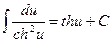19. .

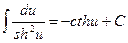Date: 2015-04-23; view: 543; Нарушение авторских прав