Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Глава 7. Обыкновенные дифференциальные уравнения
|
|
Основные понятия об уравнениях первого порядка
Определение. Обыкновенным дифференциальным уравнением n-го порядка называется соотношение вида
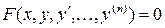, (1)
где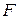 
- функция, определенная в некоторой области 
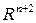, x - независимая переменная, 
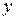- искомая функция переменной x, а 
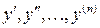- ее производные.
Порядком дифференциального уравнения называется порядок наивысшей производной, явно входящей в это уравнение. Решением дифференциального уравнения (1) называется функция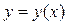 
, которая при подстановке в дифференциальное уравнение обращает его в тождество. Процесс отыскания решений дифференциального уравнения называется интегрированием уравнения. График решения дифференциального уравнения называется интегральной кривой этого уравнения.
Общий вид уравнения первого порядка следующий:
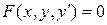. (2)
Если уравнение (2) удается разрешить относительно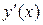 
, то получим уравнение первого порядка, разрешенное относительно производной:
.
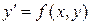Теорема (о существовании и единственности решения дифференциального уравнения первого порядка). Если в уравнении 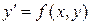функция 
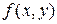и ее частная производная 
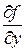непрерывны в некоторой области 
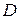, содержащей точку 
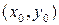на плоскости Oxy, то в некоторой окрестности точки 
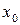существует единственное решение этого уравнения 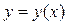, удовлетворяющее условию: 
.
Геометрический смысл теоремы заключается в том, что в указанной окрестности существует и притом единственная интегральная кривая уравнения, проходящая через точку .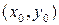
Условие, что при 
функция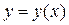 
должна равняться заданному числу 
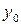, называется начальным условием. Оно записывается в виде 
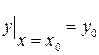или . Задача отыскания решения уравнения, удовлетворяющего начальному условию, носит название задачи Коши.
Определение.Общим решением дифференциального уравнения первого порядка называется функция
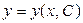, (3)
удовлетворяющая следующим условиям:
1) она является решением дифференциального уравнения при любом конкретном значении постоянной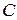 
;
2) для любых начальных условий 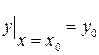, где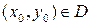 
можно найти такое значение 
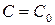, что функция 
удовлетворяет данному начальному условию.
Равенство вида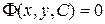 
, неявно задающее общее решение, называется общим интегралом дифференциального уравнения. Решение, полученное из общего решения (интеграла) дифференциального уравнения при фиксированном С называется частным решением(интегралом) этого уравнения.
Date: 2015-04-23; view: 515; Нарушение авторских прав