Производные и дифференциалы высших порядков

Частной производной k–го порядка функции 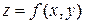называется частная производная от одной из ее производных порядка.

Сама функция 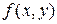считается производной нулевого порядка. Перечислим четыре производных второго порядка:

, , , .

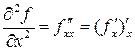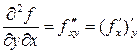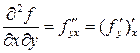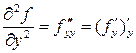Производных 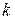–го порядка у функции двух переменных имеется .

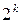Частная производная функции, в которой присутствуют дифференцирования по разным переменным, называется смешанной производной. Смешанными производными второго порядка у функции двух переменных являются 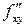и .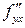

Теорема о смешанных производных. Пусть функция 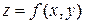и ее производные 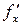, , 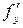, 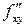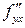непрерывны в некоторой окрестности точки 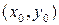. Тогда в этой точке ее смешанные производные второго порядка равны между собой:

.

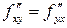Следствие. Пусть все частные производные функции

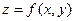
до –го порядка включительно и все ее смешанные производные 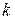–го порядка непрерывны в некоторой окрестности точки 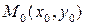. Тогда в этой точке ее смешанные производные 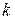–го порядка, отличающиеся только очередностью дифференцирования, совпадают.

Функция 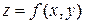, имеющая все непрерывные частные производные до 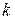–го порядка включительно в окрестности точки 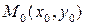, называется k раз дифференцируемой в этой точке.

Date: 2015-04-23; view: 658; Нарушение авторских прав