Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Несобственные интегралы
|
|
5.1. Пусть функция 
непрерывна в промежутке 
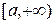. Несобственным интегралом от a до 
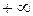от этой функции называется предел:
.
Если этот предел существует (равен числу), то несобственный интеграл называется сходящимся; если он не существует, то интеграл называется расходящимся. В случае, если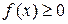 
в промежутке 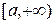, такой интеграл выражает площадь неограниченной фигуры с границами: 
, 
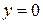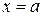
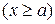и графиком функции 
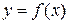. Для сходящегося интеграла эта площадь конечна, для расходящегося – бесконечна. Формула Ньютона-Лейбница для таких несобственных интегралов имеет вид:
.
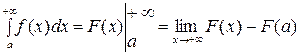5.2. Пусть теперь функция 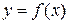непрерывна в промежутке 
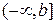. Тогда несобственным интегралом от 
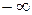до b называется предел
.
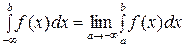Такой интеграл (при 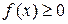) выражает площадь фигуры с границам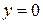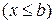и:
, 
и .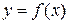
Формула Ньютона-Лейбница: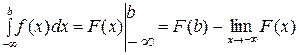 
.
5.3. Если функция 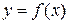непрерывна на всей числовой оси, то несобственным интегралом от 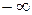до 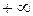называется следующая сумма двух интегралов
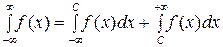
(здесь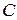 
- некоторое число). Это определение не зависит от выбора 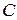. Такой интеграл называется сходящимся, если сходятся оба интеграла:
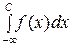и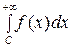 
.
Если хотя бы один из этих интегралов расходится, то интеграл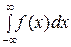 
называется расходящимс я. При 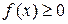интеграл 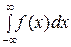выражает площадь области с границам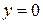и и .
Формула Ньютона-Лейбница: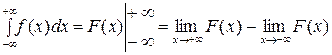 
.
Date: 2015-04-23; view: 499; Нарушение авторских прав