Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Свойства определенного интеграла
|
|
В дальнейшем будем считать, что все рассматриваемые функции – интегрируемы в соответствующих отрезках.
1) 
, 
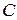- постоянная.
2) Если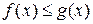 
на 
, то 
.
3) Оценка определенного интеграла снизу и сверху. Если на отрезке функция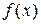 
ограничена снизу и сверху числами m и 
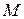, т.е. если на 
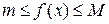, то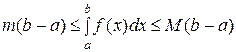 
.
4) Теорема о среднем. Пусть функция 
непрерывна на отрезке , тогда на этом отрезке найдется такая точка c, что
.
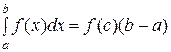Это значение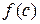 
называется средним значением функции на .
5) Оценка модуля определенного интеграла.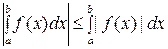 
.
6) Свойство линейности.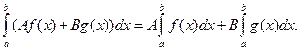 
6) Свойство аддитивности. Если выполняется неравенств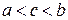о 
, то
.
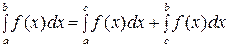Если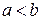 
, то интегралом 
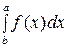называется число 
. Интеграл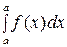 
считается равным нулю. Свойство аддитивности справедливо (при условии существования интегралов) для чисел 
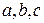расположенных в любом порядке, т.е. требование 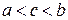здесь не обязательно.
Теорема 1. (Ньютона - Лейбница) Пусть функция непрерывна на отрезке и функция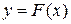 
есть ее первообразная на этом отрезке, тогда
.
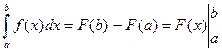Теорема 2. (Замена переменной в определенном интеграле) Пусть функция непрерывна в отрезке , а функция 
монотонная и непрерывно дифференцируема в отрезк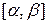е 
, где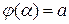 
, 
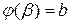, тогда
.
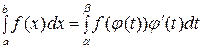Теорема 3. (Нахождение определенного интеграла по частям) Пусть функци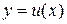и 
и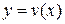 
непрерывно дифференцируемы в отрезке , тогда верно равенство
.
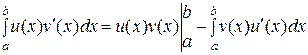Сокращенная запись: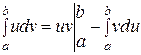 
.
Date: 2015-04-23; view: 1192; Нарушение авторских прав