
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Частные приращения и частные производные
|
|
Определение.Частным приращением по x функции 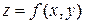 в точке
в точке 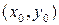 соответствующим приращению
соответствующим приращению 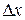 называется разность
называется разность
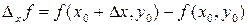 .
.
Аналогично, частным приращением по 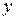 в точке
в точке 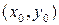 функции
функции 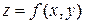 соответствующим приращению
соответствующим приращению  называется разность
называется разность
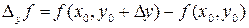 .
.
Определение. Частной производной по x функции 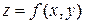 в точке
в точке 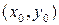 называется предел отношения частного приращения по x этой функции в указанной точке к приращению
называется предел отношения частного приращения по x этой функции в указанной точке к приращению 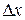 аргумента x, т.е.
аргумента x, т.е.
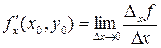 .
.
Такие частные производные обозначаются символами 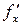 ,
, 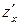 ,
, 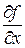 ,
,  . В последних случаях круглая буква “
. В последних случаях круглая буква “ 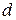 ” – “
” – “ 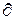 ” означает слово “частная”.
” означает слово “частная”.
Аналогично, частная производная по 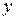 в точке
в точке 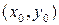 определяется с помощью предела
определяется с помощью предела
 .
.
Другие обозначения этой частной производной: 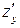 ,
, 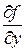 ,
, 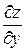 .
.
Частные производные функций находятся по известным правилам дифференцирования функции одной переменной, при этом все переменные, кроме той, по которой дифференцируется функция, считаются постоянными. Так при нахождении 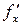 для функции
для функции 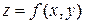 переменная
переменная 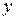 принимается за постоянную, а при нахождении
принимается за постоянную, а при нахождении 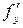 - постоянная x.
- постоянная x.
Если функция 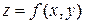 имеет частные производные, то ее частными дифференциалами называются выражения
имеет частные производные, то ее частными дифференциалами называются выражения
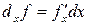 и
и 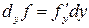 .
.
Здесь 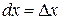 и
и 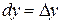 .
.
Частные дифференциалы являются дифференциалами функций одной переменной полученными из функции двух переменных 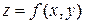 при фиксированных
при фиксированных 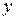 или х.
или х.
Date: 2015-04-23; view: 1776; Нарушение авторских прав