
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Монотонность и экстремумы функции
|
|
Функция 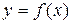 называется неубывающей (возрастающей) в интервале (а,b), если для любых
называется неубывающей (возрастающей) в интервале (а,b), если для любых 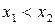 из этого интервала выполняется неравенство
из этого интервала выполняется неравенство 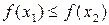 (
(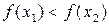 ). Если
). Если 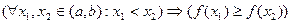 (
(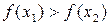 ), то такая функция называется невозрастающей (убывающей) в (а,b). Такие функции называют монотонными в интервале (а,b).
), то такая функция называется невозрастающей (убывающей) в (а,b). Такие функции называют монотонными в интервале (а,b).
Теорема. Пусть функция  дифференцируема в интервале
дифференцируема в интервале 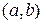 .
.
1. Если f(x) монотонно возрастает в 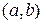 , то
, то 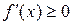 ,
, 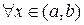 .
.
2. Если 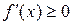 ,
, 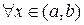 , то
, то 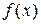 монотонно возрастает в
монотонно возрастает в 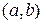 .
.
В интервалах возрастания или убывания функции знак производной не меняется.
Определение. Точка 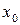 называется точкой минимума (максимума) функции
называется точкой минимума (максимума) функции  если она определена в некоторой окрестности
если она определена в некоторой окрестности 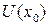 этой точки и для
этой точки и для 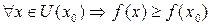
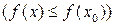 .
.
Значение 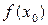 в этом случае называется минимумом (максимумом) функции. Точки минимума и максимума называются экстремальными точками, а соответствующие значения - экстремумами функции.
в этом случае называется минимумом (максимумом) функции. Точки минимума и максимума называются экстремальными точками, а соответствующие значения - экстремумами функции.
Точка x0, в которой функция y=f(x) непрерывна, а её производная 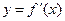 равна нулю или не существует, называется критической точкой этой функции.
равна нулю или не существует, называется критической точкой этой функции.
Теорема (необходимое условие экстремума). Пусть x0 – экстремальная точка функции y=f (x), тогда x0 – критическая точка этой функции.
Обратное утверждение к этой теореме не верно.
Теорема (достаточное условие экстремума). Пусть функция  непрерывна в окрестности U(x0) критической точки x0 и дифференцируема в U(x0)\ {x0}. Тогда
непрерывна в окрестности U(x0) критической точки x0 и дифференцируема в U(x0)\ {x0}. Тогда
1) если в U(x0) f '(x)>0 при х<x0 и f '(x)<0 при x>x0 , то x0 - точка максимума;
2) если в U(x0) f '(x)<0 при х<x0 и f '(x)>0 при x>x0 , то x0 - точка минимума;
3) если в U(x0) f ' (x)>0 или f ' (x)<0 при x¹ x0 , то в x0 экстремума нет.
Теорема. Пусть функция y=f(x) дифференцируема в некоторой окрестности критической точки х0 и вторая производная f''(x0) существует. Тогда, если f''(x0)>0, то x0 - точка минимума, а если f''(x0)<0, то x0 - точка максимума.
С помощью исследования экстремумов можно находить наибольшее и наименьшее значение функции на отрезке:
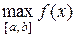 = max{ f (a), f (b), f (x i): x iÎ(a,b) - точки максимума},
= max{ f (a), f (b), f (x i): x iÎ(a,b) - точки максимума},
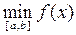 = min{ f (a), f (b), f (x i): x iÎ(a,b) - точки минимума}.
= min{ f (a), f (b), f (x i): x iÎ(a,b) - точки минимума}.
Date: 2015-04-23; view: 864; Нарушение авторских прав