
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Выпуклость и точки перегиба функции
|
|
Пусть функция  дифференцируема в интервале (a,b). Эта функция называется выпуклой вниз (вверх) в интервале (a,b), если для любого x 0Î(a,b) значение функции для " х Î(a,b) не меньше (не больше) соответствующей ординаты касательной к графику функции, проведенной в точке (x0, f (x0)) (см. рис. 1).
дифференцируема в интервале (a,b). Эта функция называется выпуклой вниз (вверх) в интервале (a,b), если для любого x 0Î(a,b) значение функции для " х Î(a,b) не меньше (не больше) соответствующей ординаты касательной к графику функции, проведенной в точке (x0, f (x0)) (см. рис. 1).
Теорема. Пусть функция y=f(x) дважды непрерывно дифференцируема в (a,b). Эта функция выпукла вниз (вверх) на этом интервале тогда и только тогда, когда f ''(x)³0 (f ''(x) 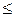 0) "xÎ(a,b).
0) "xÎ(a,b).
Точка 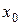 называется точкой перегиба для функции
называется точкой перегиба для функции
 , если в некоторой окрестности этой точки график функции лежит по разные стороны от касательной к графику, проведенной в точке
, если в некоторой окрестности этой точки график функции лежит по разные стороны от касательной к графику, проведенной в точке 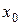 , т.е. для
, т.е. для  а для
а для 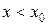
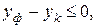 или наоборот. Точку
или наоборот. Точку 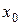 , в которой имеется вертикальная касательная, называют точкой перегиба, если направления выпуклости функции по разные стороны от
, в которой имеется вертикальная касательная, называют точкой перегиба, если направления выпуклости функции по разные стороны от 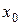 противоположны (см. рис. 2).
противоположны (см. рис. 2).
 |
 |
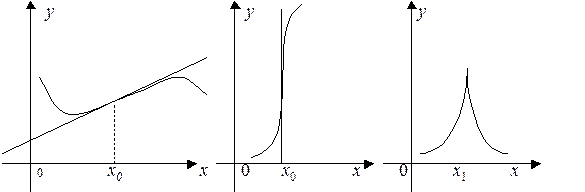 На рисунках
На рисунках 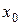 ¾ точка перегиба,
¾ точка перегиба, 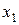 ¾ не точка перегиба
¾ не точка перегиба
Теорема (необходимое условие существования точки перегиба). Пусть функция y = f(x) дважды непрерывно дифференцируема в U(x0)\{x0} и непрерывна в точке х0. Тогда, если х0 ¾ точка перегиба, то значение f''(x0)=0 или не существует.
Такие точки х 0, в которых функция y = f(x) непрерывна, а 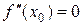 или не существует, называются критическими точками второго порядка.
или не существует, называются критическими точками второго порядка.
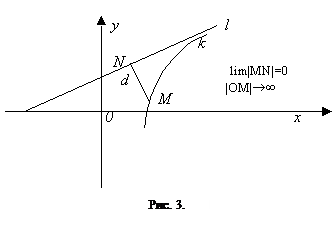 Теорема (достаточное условие существования точки перегиба). Пусть функция
Теорема (достаточное условие существования точки перегиба). Пусть функция  дважды непрерывно дифференцируема в U(x0)\{x0} и непрерывна в x0, где x0 – критическая точка второго порядка. Тогда, если при x<x0 и x>x0, f ''(x) имеет разные знаки, то x0 – точка перегиба этой функции. Если же при x<x0 и x>x0, знаки f ''(x) совпадают, x0 – не точка перегиба.
дважды непрерывно дифференцируема в U(x0)\{x0} и непрерывна в x0, где x0 – критическая точка второго порядка. Тогда, если при x<x0 и x>x0, f ''(x) имеет разные знаки, то x0 – точка перегиба этой функции. Если же при x<x0 и x>x0, знаки f ''(x) совпадают, x0 – не точка перегиба.
Date: 2015-04-23; view: 672; Нарушение авторских прав