
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Правило Лопиталя. Раскрытие неопределенностей
|
|
Теорема Лопиталя. Пусть  и
и 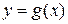 - две б.м. или б.б. при
- две б.м. или б.б. при 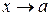 функции, дифференцируемые в окрестности
функции, дифференцируемые в окрестности 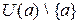 и пусть
и пусть 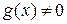 и
и 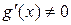 в
в 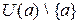 . Тогда, если существует
. Тогда, если существует 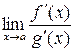 , то существует
, то существует 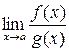 и они равны между собой:
и они равны между собой:
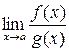 =
= 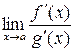 .
.
Аналогичные утверждения справедливы для  ,
, 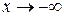 ,
, 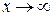 ,
,  ,
,  , а также для случая, когда функция
, а также для случая, когда функция 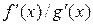 является бесконечно большой.
является бесконечно большой.
К пределам других видов – 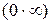 ,
, 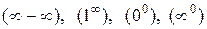 также можно применять правило Лопиталя, предварительно преобразовав выражение к виду
также можно применять правило Лопиталя, предварительно преобразовав выражение к виду 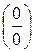 или
или  .
.
1. Произведение б.м. на б.б. функцию 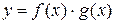 , т.е. вида
, т.е. вида 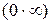 , преобразуется к виду
, преобразуется к виду
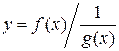 (вида
(вида 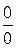 ) или
) или 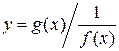 (вида
(вида 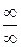 ).
).
Затем применяется правило Лопиталя.
2. Разность двух б.б. функций 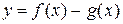 вида
вида 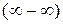 преобразуется, например, к виду
преобразуется, например, к виду
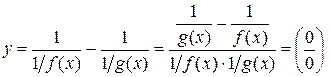 ;
;
к этому выражению применяется правило Лопиталя.
3. Функция 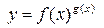 типа
типа 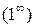 или
или 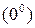 записывается в виде
записывается в виде
 ,
,
затем вычисляется 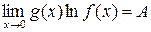 типа
типа 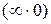 .
.
Если 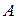 – число, то
– число, то 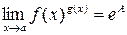 .
.
Если 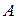 =
= 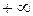 , то
, то 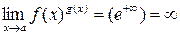 .
.
Если 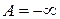 , то
, то 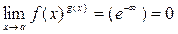 .
.
Исследование функций с помощью производных
Date: 2015-04-23; view: 626; Нарушение авторских прав