Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Механический и геометрический смыслы производной
|
|
2.1. Пусть некоторая точка движется вдоль прямой и за время t проходит путь S(t). Тогда за промежуток времени от 
до 
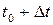она проходит путь 
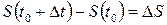, и средняя скорость точки на промежутке 
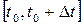равна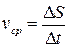 
. Мгновенная скорость v точки в момент равна пределу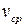 
при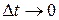 
: 
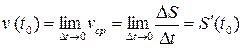. Итак, мгновенная скорость точки в момент равна производной от пути, проходимого этой точкой по времени при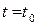 
. Это и есть механический смысл производной.
2.2. Проведём прямую через две точк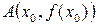и 
и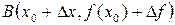 
, лежащие на графике функции 
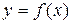. Эта прямая называется секущей к графику функции (рис. 2). Её угловой коэффициент, т. е. тангенс угла наклона к оси Оx равен
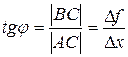. (2)
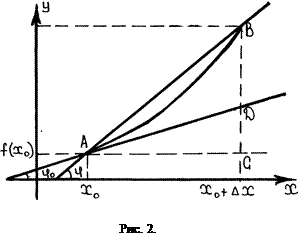Определение. Касательной к графику функции 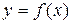в точке 
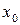называется прямая, являющаяся предельным положением секущей, проходящей через точку A 
при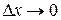 
.
Касательная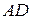 
в точке - это прямая, проходящая через , угловой коэффициент которой равен 
.
Таким образом,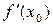 
есть угловой коэффициент касательной к графику 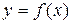в точке (геометрический смысл производной).
Уравнение этой касательной имеет вид: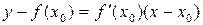 
Date: 2015-04-23; view: 650; Нарушение авторских прав