
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Кривые второго порядка на плоскости
|
|
1. Эллипс. Пусть на плоскости 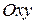 имеются две точки
имеются две точки 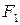 и
и 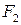 , называемые фокусами на расстоянии
, называемые фокусами на расстоянии 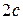 друг от друга (
друг от друга (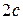 – фокусное расстояние). Расположим их на оси
– фокусное расстояние). Расположим их на оси 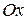 симметрично относительно начала координат, т.е.
симметрично относительно начала координат, т.е. 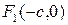 и
и 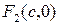 . Пусть
. Пусть 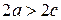 .
.
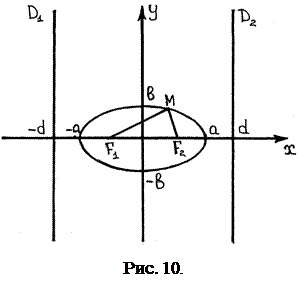 Определение. Эллипсом называется геометрическое место точек
Определение. Эллипсом называется геометрическое место точек 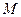 плоскости, сумма расстояний, от которых до двух выбранных фокусов, постоянна и равна
плоскости, сумма расстояний, от которых до двух выбранных фокусов, постоянна и равна 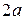 (см. рис. 10).
(см. рис. 10).
Уравнение 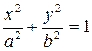 , где
, где 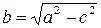 называется каноническим уравнением эллипса, а числа а и
называется каноническим уравнением эллипса, а числа а и 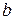 - его полуосями (большой и малой).
- его полуосями (большой и малой).
Точки пересечения этого эллипса с осями координат называются вершинами эллипса.
Ось, проходящая через фокусы эллипса (ось 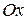 ) называется его фокальной осью. Число
) называется его фокальной осью. Число 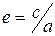 называется эксцентриситетом. У эллипса
называется эксцентриситетом. У эллипса 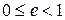 .
.
2. Окружность. В частном случае, когда фокусное расстояние эллипса 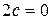 , два фокуса эллипса совпадают с его центром. При этом
, два фокуса эллипса совпадают с его центром. При этом 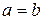 и эллипс превращается в окружность радиуса a с каноническим управлением:
и эллипс превращается в окружность радиуса a с каноническим управлением:
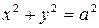 .
.
Уравнение окружности радиуса a с центром в точке 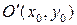 имеет вид:
имеет вид: 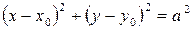 .
.
3. Гипербола. Пусть на плоскости имеются два фокуса (например, 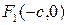 и
и 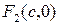 ) и пусть
) и пусть 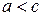 .
.
Определение. Гиперболой называется геометрическое место точек 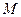 плоскости, разность расстояний от которых до двух выбранных фокусов постоянна и равна
плоскости, разность расстояний от которых до двух выбранных фокусов постоянна и равна  .
.
Каноническое уравнение гиперболы:
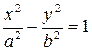 , где
, где 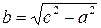 .
.
 Число а называется действительной полуосью этойгиперболы, а число
Число а называется действительной полуосью этойгиперболы, а число 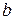 – ее мнимой полуосью.
– ее мнимой полуосью.
Гипербола пересекает ось 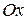 в точках
в точках  и
и 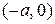 . Эти точки называются вершинами гиперболы.
. Эти точки называются вершинами гиперболы.
Определения эксцентриситета гиперболы повторяют соответствующие определения для эллипса. Эксцентриситет гиперболы 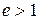 .
.
Определение. Прямая 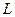 называется асимптотой кривой
называется асимптотой кривой 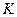 , если расстояние от точки на кривой до этой прямой стремится к нулю при удалении точки вдоль кривой в бесконечность.
, если расстояние от точки на кривой до этой прямой стремится к нулю при удалении точки вдоль кривой в бесконечность.
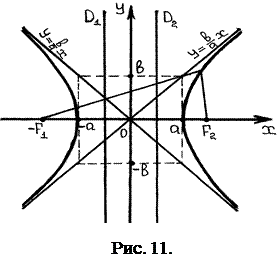
Прямые 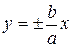 являются асимптотами обеих ветвей гиперболы
являются асимптотами обеих ветвей гиперболы 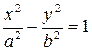 (см. рис. 11).
(см. рис. 11).
 4. Парабола. Пусть на плоскости имеется прямая
4. Парабола. Пусть на плоскости имеется прямая 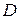 (директриса) и точка
(директриса) и точка 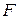 (фокус) на расстоянии
(фокус) на расстоянии 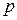 от директрисы. Пусть
от директрисы. Пусть 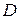 имеет уравнение
имеет уравнение 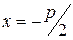 , фокус - координаты
, фокус - координаты 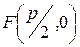 .
.
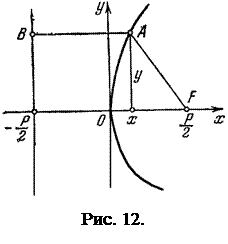
Определение. Параболой называется геометрическое место точек 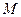 плоскости, расстояние от которых до фокуса совпадает с расстоянием до директрисы (см. рис. 12).
плоскости, расстояние от которых до фокуса совпадает с расстоянием до директрисы (см. рис. 12).
Уравнение 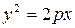 называется каноническим уравнением параболы, а число
называется каноническим уравнением параболы, а число 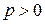 - ее параметром. Эта парабола проходит через т.
- ее параметром. Эта парабола проходит через т. 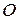 , которая называется ее вершиной.Эксцентриситет
, которая называется ее вершиной.Эксцентриситет 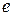 параболы всегда считается равным единице. Асимптот у параболы нет.
параболы всегда считается равным единице. Асимптот у параболы нет.
§10. Основные понятия об n -мерном арифметическом пространстве 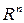
1. Определение. n-мерным арифметическим пространством 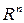 называется множество всех строк (или столбцов), состоящих из n действительных чисел.
называется множество всех строк (или столбцов), состоящих из n действительных чисел.
Строка 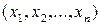 называется точкой в
называется точкой в 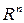 , а числа
, а числа 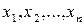 ее координатами в стандартной системе координат. Точка
ее координатами в стандартной системе координат. Точка 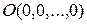 называется началом координат, а множество точек вида
называется началом координат, а множество точек вида 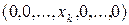 -
- 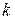 -ой координатной осью (обозначается
-ой координатной осью (обозначается 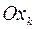 ). Здесь
). Здесь 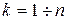 . Расстоянием от точки
. Расстоянием от точки 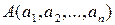 до точки
до точки 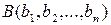 в
в 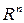 (или, что тоже самое, длиной отрезка
(или, что тоже самое, длиной отрезка 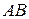 ) называется число
) называется число
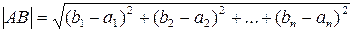 .
.
Вектором в 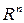 с началом в точке
с началом в точке 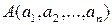 и концом в точке
и концом в точке 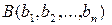 называется строка (или столбец), составленная из разностей координат точек
называется строка (или столбец), составленная из разностей координат точек 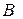 и
и 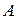 :
:
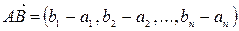 .
.
Над векторами в 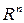 определяются операции сложения и умножения на числа по соответствующим правилам, определенным в §2 для матриц.
определяются операции сложения и умножения на числа по соответствующим правилам, определенным в §2 для матриц.
Единичные векторы, направленные вдоль координатных осей, т. е. векторы 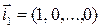 ,
, 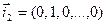 , …,
, …, 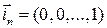 называются стандартным базисом в
называются стандартным базисом в 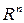 , числа
, числа 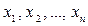 - координатами вектора
- координатами вектора 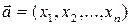 в стандартном базисе
в стандартном базисе 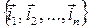 . При этом очевидно равенство
. При этом очевидно равенство 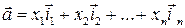 .
.
2. Скалярным произведением векторов 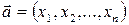 и
и 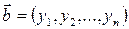 в
в 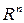 называется число
называется число 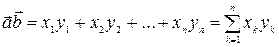 .
.
Модулем вектора 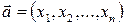 называется число
называется число
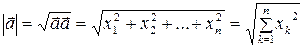 .
.
Векторы 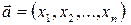 и
и 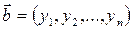 называются перпендикулярными, если их скалярное произведение равно нулю:
называются перпендикулярными, если их скалярное произведение равно нулю:  .
.
Теорема (Неравенство Буняковского). Для любых векторов 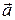 и
и 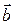 из
из 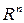 справедливо неравенство
справедливо неравенство 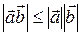 .
.
Углом между векторами 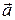 и
и 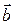 в
в 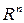 называется такой угол
называется такой угол  , что
, что
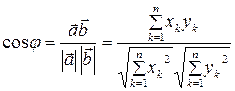 .
.
3. Гиперплоскостью в 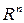 называется множество всех его точек, координаты
называется множество всех его точек, координаты 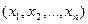 которых удовлетворяют уравнению
которых удовлетворяют уравнению
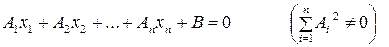 .
.
Date: 2015-04-23; view: 765; Нарушение авторских прав