Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Прямая на плоскости. 1. Уравнение прямой с угловым коэффициентомимеет вид:
|
|
1. Уравнение прямой с угловым коэффициентом имеет вид:
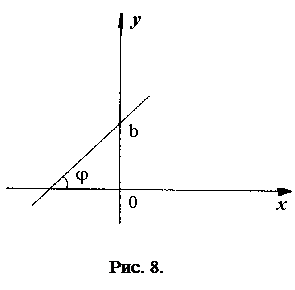
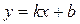
Здесь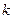 
- тангенс угла наклона этой прямой к оси 
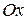и 
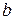– ордината точки пересечения прямой с осью 
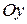(см. рис. 8). С помощью такого уравнения можно задать любую прямую не перпендикулярную оси .
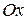Теорема. Тангенс угла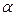 
между прямым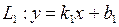и 
и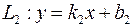 
определяется формулой
.
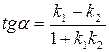Прямые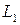 
и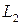 
параллельны только в том случае когда 
.
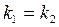Прямые 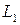и 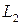перпендикулярны только в том случае, когда 
.
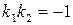2. Общее уравнение прямой: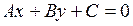 
.
Теорема. Любая прямая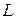 
на плоскости 
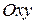определяется своим общим уравнением и любое уравнение вида 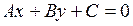, где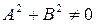 
задает некоторую прямую на плоскости.
Вектор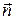 
перпендикулярный прямой 
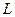называется нормальным вектором этой прямой.
Теорема о нормальном векторе прямой. Вектор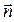 
с координатами 
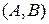является нормальным для прямой 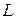с уравнением 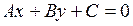на плоскости .
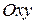Следствие 1. Косинус угла 
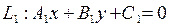между прямыми 
и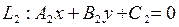 
с нормальными векторами 
и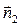 
соответственно, находится по формуле:
.
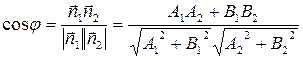Следствие 2. Эти прямые перпендикулярны только в том случае, когда
.
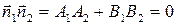Следствие 3. Эти прямые параллельны только в том случае, когда
.
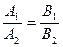Если же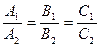 
, то прямые 
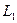и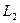 
совпадают
Date: 2015-04-23; view: 548; Нарушение авторских прав