
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Скалярное произведение векторов и его свойства. Определение. Скалярным произведением векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними
|
|
Определение. Скалярным произведением векторов 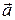 и
и 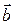 называется число, равное произведению модулей этих векторов на косинус угла между ними, т. е.
называется число, равное произведению модулей этих векторов на косинус угла между ними, т. е.
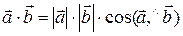 .
.
Для любых векторов справедливы следующие свойства.
1) 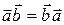 .
.
2)  , т. к.
, т. к. 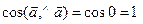 .
.
3) Скалярное произведение ненулевых векторов 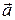 и
и 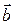 равно
равно  только в том случае, когда эти векторы ортогональны (перпендикулярны).
только в том случае, когда эти векторы ортогональны (перпендикулярны).
Проекцией вектора 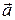 на ненулевой вектор
на ненулевой вектор 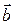 (обозначение
(обозначение 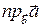 ) называется его проекция на ось l, проведенную через вектор
) называется его проекция на ось l, проведенную через вектор 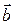 (см. рис. 5).
(см. рис. 5).
 4)
4)  .
.
5) Для любого вектора 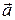 с координатами
с координатами 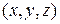 в базисе
в базисе  верно:
верно:
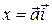 ,
, 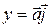 ,
, 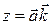 .
.
6) 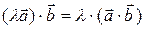 ; λ – любое число.
; λ – любое число.
7) 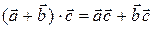 .
.
Теорема. Пусть в базисе  вектор
вектор 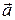 имеет координаты
имеет координаты  , а вектор
, а вектор 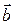 –
–  . Тогда
. Тогда
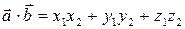 .
.
Следствие 1. Модуль вектора 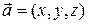 равен
равен  .
.
Следствие 2. Косинус угла  между векторами
между векторами 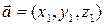 и
и 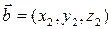 равен
равен
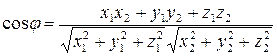 .
.
Следствие 3. Ненулевые векторы 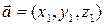 и
и 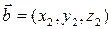 перпендикулярны только в том случае, когда
перпендикулярны только в том случае, когда
 .
.
Date: 2015-04-23; view: 629; Нарушение авторских прав