Смешанное произведение векторов. Определение.Смешанным произведением трех векторов называется число, равное скалярному произведению векторного произведения векторов с вектором : ( )

Определение.Смешанным произведением трех векторов называется число, равное скалярному произведению векторного произведения векторов 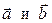с вектором : ().

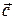Основные его свойства заключаются в следующей теореме (свойство 1).

1.Теорема. Смешанное произведение векторов равно объему параллелепипеда, построенного на этих векторах:

Здесь знак “+” берется, в случае, если тройка векторов 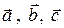- правая, “-” если она левая (см. рис. 7).

2. Векторы 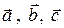- являются компланарными только в том случае, когда их смешанное произведение равно 0: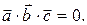

3. .

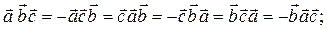
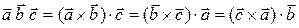4. ,. λ число.

5. .

Теорема. Пусть в базисе 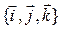векторы 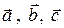имеют координаты соответственно , 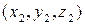и , тогда их смешанное произведение записывается в виде определителя:

.

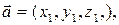
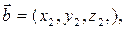
Следствие. Объем параллелепипеда, построенного на векторах 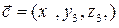равен:

.

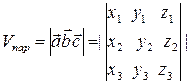Объем тетраэдра (треугольной пирамиды), образованного этими векторами, равен:

.

Date: 2015-04-23; view: 620; Нарушение авторских прав