
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Базис векторного пространства. Координаты вектора
|
|
Векторным пространством называется такое множество векторов, что любая линейная комбинация векторов этого множества также ему принадлежит.
Определение. Любой ненулевой вектор 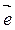 на прямой называется базисным вектором этой прямой. Любая пара неколлинеарных векторов {
на прямой называется базисным вектором этой прямой. Любая пара неколлинеарных векторов { 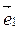 ,
,  } плоскости называется базисом этой плоскости. Любая тройка некомпланарных векторов {
} плоскости называется базисом этой плоскости. Любая тройка некомпланарных векторов { 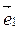 ,
,  ,
, 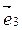 } называется базисом пространства.
} называется базисом пространства.
Теорема о базисе. Любой вектор  (на прямой, плоскости или в пространстве) единственным образом записывается в виде линейной комбинации соответствующих базисных векторов. То есть,
(на прямой, плоскости или в пространстве) единственным образом записывается в виде линейной комбинации соответствующих базисных векторов. То есть,
1) на прямой:  =x
=x 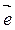 ,
,
2) на плоскости:  =x
=x 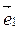 +y
+y  ,
,
3) в пространстве:  = x
= x 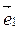 + y
+ y  + z
+ z 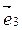
Определение. Коэффициенты линейной комбинации базисных векторов выражающих вектор  на прямой, в плоскости или в пространстве называются координатами вектора
на прямой, в плоскости или в пространстве называются координатами вектора  в данном базисе.
в данном базисе.
Date: 2015-04-23; view: 626; Нарушение авторских прав