
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число
|
|
Пусть в пространстве имеется, декартова система координат  . С ней связан стандартный базис из единичных взаимно перпендикулярных векторов, расположенных вдоль осей Ox, Oy, Oz. Эти базисные вектора обозначаются через
. С ней связан стандартный базис из единичных взаимно перпендикулярных векторов, расположенных вдоль осей Ox, Oy, Oz. Эти базисные вектора обозначаются через 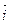 ,
, 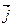 ,
, 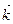 . Вектор, начало которого находится в начале координат - точке О, а конец в точке А, т. е. вектор
. Вектор, начало которого находится в начале координат - точке О, а конец в точке А, т. е. вектор 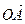 , называется радиус-вектором точки А.
, называется радиус-вектором точки А.
Если (x,y,z) – координаты точки A в системе  , то радиус-вектор
, то радиус-вектор 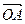 можно записать в виде
можно записать в виде 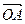 = x
= x 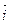 +y
+y 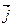 +z
+z 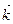 . Координаты точки A(x,y,z) в системе
. Координаты точки A(x,y,z) в системе  и вектора
и вектора 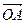 в базисе
в базисе 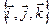 – это одни и те же числа.
– это одни и те же числа.
Теорема. Пусть в декартовой системе координат  заданы две точки
заданы две точки 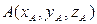 и
и 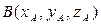 , тогда в базисе
, тогда в базисе 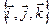 вектор
вектор  имеет координаты
имеет координаты 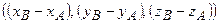 .
.
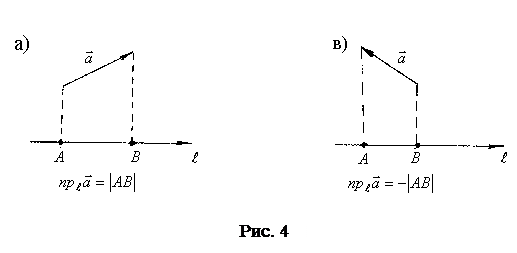 |
Определение.Проекцией вектора
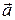 на координатную ось
на координатную ось 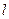 (
( 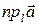 ) называется длина проекции вектора
) называется длина проекции вектора 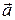 на
на 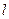 взятая со знаком “+”, если угол между
взятая со знаком “+”, если угол между 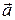 и положительным направлением оси острый, и “–“, если он тупой (см. рис. 4).
и положительным направлением оси острый, и “–“, если он тупой (см. рис. 4).
Если λ – число, 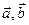 - векторы, то
- векторы, то 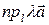 =
= 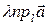 и
и 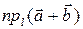 =
= 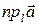 +
+ 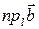 .
.
Теорема. Пусть вектор 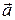 имеет координаты
имеет координаты 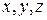 в базисе
в базисе  , тогда
, тогда 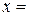
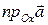 ,
, 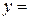
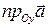 ,
, 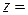
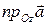 .
.
Date: 2015-04-23; view: 846; Нарушение авторских прав