
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Векторы и линейные операции над ними
|
|
Определение. Вектором с началом в точке A и с концом в точке B называется отрезок с выбранным направлением, или направленный отрезок - 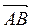 .
.
Вектор, у которого начало совпадает с его концом, называется нулевым вектором - 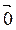 . Длина отрезка, изображающего вектор
. Длина отрезка, изображающего вектор 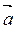 называется модулем этого вектора - |
называется модулем этого вектора - | 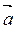 |. Векторы
|. Векторы 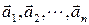 параллельные одной прямой называются коллинеарными. Нулевой вектор считается коллинеарным любым векторам. Два вектора
параллельные одной прямой называются коллинеарными. Нулевой вектор считается коллинеарным любым векторам. Два вектора 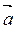 и
и 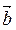 считаются равными, если они равны по модулю, коллинеарны и одинаково направлены.
считаются равными, если они равны по модулю, коллинеарны и одинаково направлены.
Определение.Произведением вектора 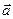 на число a называется такой вектор
на число a называется такой вектор 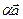 , что выполняются три условия.
, что выполняются три условия.
1) |a 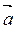 |=|a||
|=|a|| 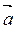 |, 2)a
|, 2)a 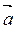 ||
|| 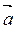 ,
,
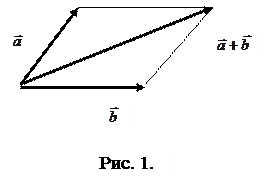 3) Вектор a
3) Вектор a  сонаправлен вектору
сонаправлен вектору 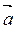 , если a>0 и направлен в противоположную сторону, если a<0.
, если a>0 и направлен в противоположную сторону, если a<0.
Определение (правило паралле-лограмма). Суммой векторов 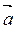 и
и 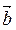 , исходящих из одной точки, называется вектор, совпадающий с диагональю параллелограмма образованного векторами
, исходящих из одной точки, называется вектор, совпадающий с диагональю параллелограмма образованного векторами 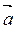 и
и 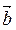 , исходящий из той же точки (см. рис. 1).
, исходящий из той же точки (см. рис. 1).
Суммой векторов 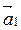 ,
, 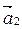 ,...,
,..., 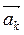 , у которых начало вектора
, у которых начало вектора 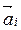 совпадает с концом
совпадает с концом 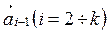 , является вектор, соединяющий начало вектора
, является вектор, соединяющий начало вектора 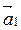 с концом вектора
с концом вектора  (см. рис. 2).
(см. рис. 2).
Эти линейные операции над векторами обладают следующими свойствами. 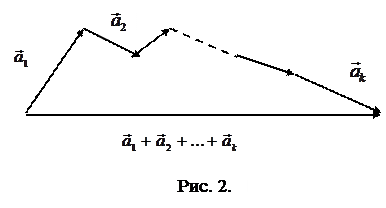
1. 1×  =
=  .
.
2. 0×  =
= 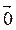 .
.
3. a(b  )=(ab)
)=(ab)  .
.
4. (a+b)  =a
=a  +b
+b  .
.
5.  +
+ 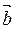 =
= 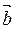 +
+  .
.
6. ( +
+ 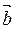 )+
)+ 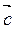 =
=  +(
+(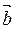 +
+ 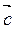 ).
).
7. a( +
+ 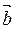 )=a
)=a  +a
+a 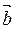
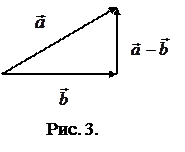 Разностью векторов
Разностью векторов  и
и 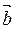 , исходящих из одной точки называется вектор, соединяющий конец вектора
, исходящих из одной точки называется вектор, соединяющий конец вектора 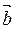 с концом вектора
с концом вектора  (см. рис. 3).
(см. рис. 3).
Определение. Линейной комбинацией векторов 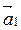 ,
, 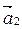 ,...,
,..., 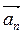 с коэффициентами C1,C2,...,Cn называется вектор C1
с коэффициентами C1,C2,...,Cn называется вектор C1 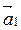 +C2
+C2 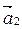 +...+Cn
+...+Cn 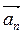 .
.
Если векторы 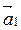 ,
, 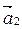 ,...,
,..., 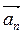 коллинеарны некоторой прямой, то любая их линейная комбинация будет коллинеарна той же прямой.
коллинеарны некоторой прямой, то любая их линейная комбинация будет коллинеарна той же прямой.
Векторы 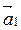 ,
, 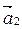 ,...,
,..., 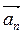 параллельные одной плоскости называются компланарными. Если векторы
параллельные одной плоскости называются компланарными. Если векторы 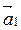 ,
, 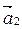 ,...,
,..., 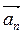 компланарны некоторой плоскости, то любая их линейная комбинация компланарна той же плоскости.
компланарны некоторой плоскости, то любая их линейная комбинация компланарна той же плоскости.
Date: 2015-04-23; view: 611; Нарушение авторских прав