Метод Гаусса для исследования и решения СЛАУ

Расширенной матрицей СЛАУ называется матрица, полученная из матрицы системы приписыванием справа столбца свободных членов системы:

= .

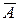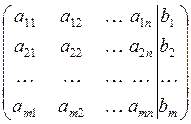Элементарными преобразованиями для матрицы 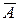называются следующие её преобразования.

1. Перестановка строк местами.

2. Умножение строки на ненулевой коэффициент.

3. Прибавление к одной строке матрицы другой её строки умноженной на некоторое число .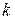

4. Зачёркивание нулевой строки матрицы.

Метод Гаусса состоит в том, что с помощью элементарных преобразований матрица 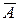приводится к верхнетреугольному виду с ненулевыми элементами на главной диагонали.

1. С помощью перестановок строк и столбцов матрицы добиваемся того, чтобы a₁₁ стал отличным от нуля (здесь и в дальнейшем элементы всех матриц будем обозначать в виде a_ij).

2. Прибавим ко второй строке первую, умноженную на 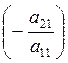. Прибавим к третьей строке матрицы первую, умноженную на 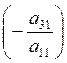и так далее. В результате в первом столбце получим нулевые элементы ниже a₁₁.

3. С помощью перестановок строк и столбцов, начиная со второй строки и второго столбца, добиваемся того, чтобы a₂₂ ¹0.

4. Прибавим к третьей строке вторую, умноженную на 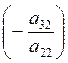. Прибавим к четвёртой строке матрицы вторую, умноженную на 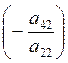и так далее. В результате во втором столбце получим нулевые элементы ниже a₂₂.

Этот процесс продолжаем до тех пор, пока возможно получение 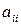¹0 из строк и столбцов начиная с номера .

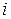Окончательно, после зачёркивания нулевых строк матрица приводится к виду 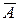~ , где все 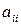¹ 0.

После приведения матрицы 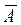к верхнетреугольному виду, по последней матрице восстанавливаем систему и решаем её, начиная с последнего уравнения. Возможны три случая.

1) Система решений не имеет.

2) Система имеет единственное решение.

3) Система имеет бесконечно много решений, зависящих от нескольких произвольных параметров.

Date: 2015-04-23; view: 587; Нарушение авторских прав