
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основное состояние осциллятора
|
|
По определению, основное состояние квантовой частицы есть состояние с минимальной энергией, которое в случае квантового осциллятора соответствует состоянию с 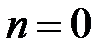 :
:
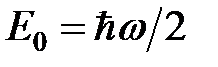 . (8)
. (8)
Уровень 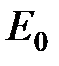 называют нулевой энергией осциллятора. Существование нулевых колебаний с энергией
называют нулевой энергией осциллятора. Существование нулевых колебаний с энергией 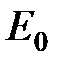 связано непосредственно с соотношением неопределённости Гейзенберга, из которого следует невозможность абсолютной локализации частицы, т.е. ситуации, когда
связано непосредственно с соотношением неопределённости Гейзенберга, из которого следует невозможность абсолютной локализации частицы, т.е. ситуации, когда 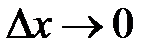 .
.
Точки пересечения потенциальной энергии 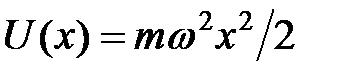 с уровнем
с уровнем 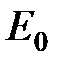 есть классические точки поворота
есть классические точки поворота 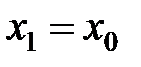 ,
, 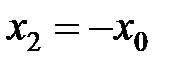 . Таким образом,
. Таким образом, 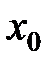 есть амплитуда классического осциллятора с энергией
есть амплитуда классического осциллятора с энергией 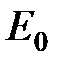 . Эта величина выбрана как единица измерения координаты квантового осциллятора:
. Эта величина выбрана как единица измерения координаты квантового осциллятора: 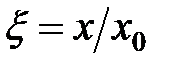 .
.
Волновую функцию основного состояния можно получить из общей формулы (5) при 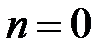 :
: 
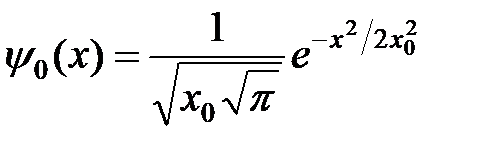 . (9)
. (9)
Возбуждённые состояния осциллятора
Волновые функции первых двух возбуждённых состояний получим из (5) при 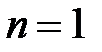 и 2:
и 2:
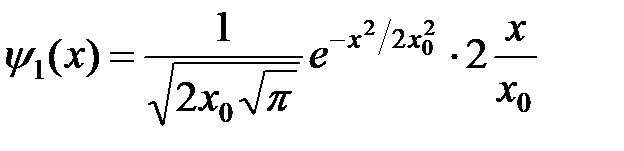 ,
,
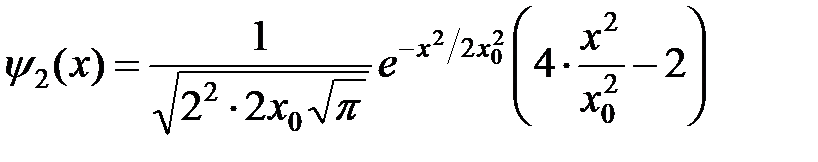 .
.
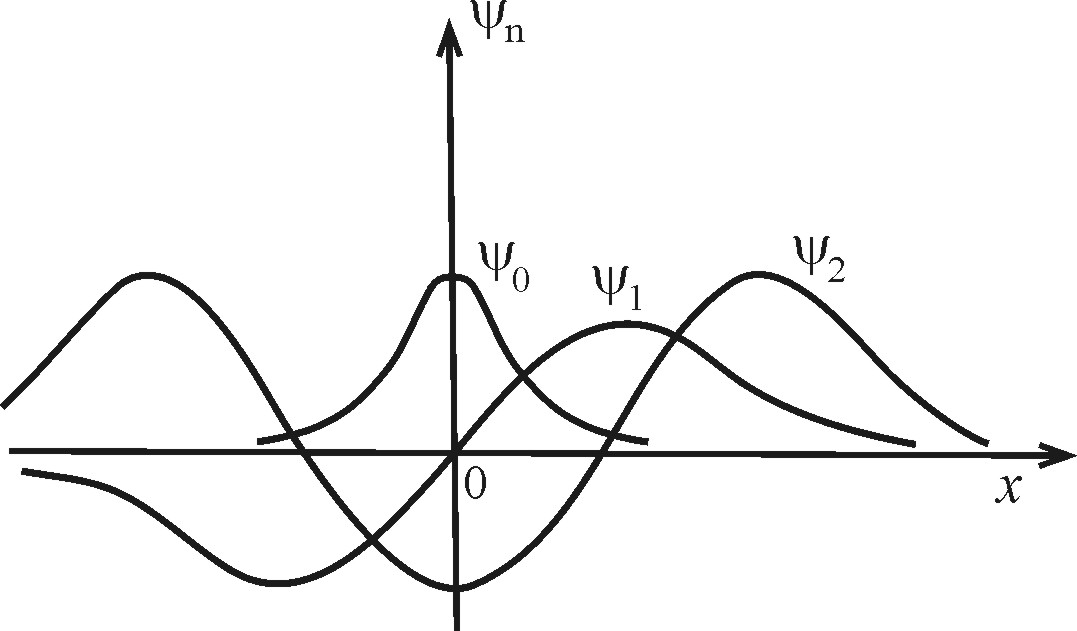
На рисунке представлены волновые функции 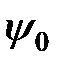 ,
, 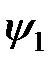 и
и 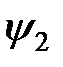 .
.
|
Рис. 2.12. Волновые функции основного 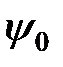 и первых двух возбужденных состояний и первых двух возбужденных состояний 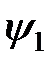 и и 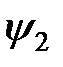 квантового гармонического осциллятора. квантового гармонического осциллятора.
|
На рис. 2.13 представлены квантовые плотности распределения для осциллятора 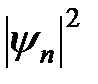 . Видно, что при малых квантовых числах плотность вероятности существенно отличается от классической функции распределения, но в пределе больших квантовых чисел
. Видно, что при малых квантовых числах плотность вероятности существенно отличается от классической функции распределения, но в пределе больших квантовых чисел 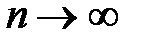 квантовая функция распределения стремится к классической, что соответствует предельному переходу от квантовой к классической механике при больших значениях
квантовая функция распределения стремится к классической, что соответствует предельному переходу от квантовой к классической механике при больших значениях 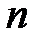 .
.
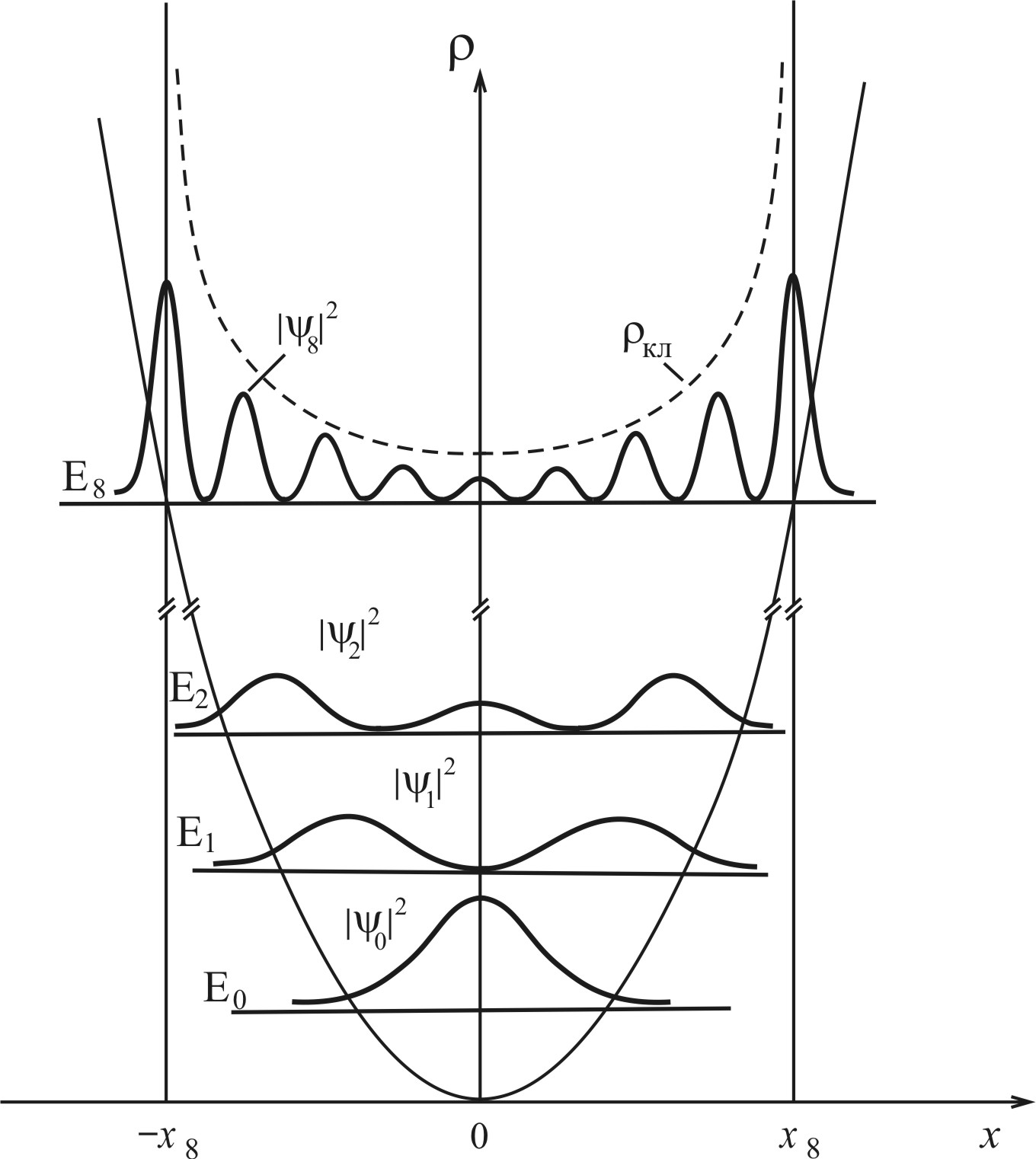
Рис. 2.13. Сравнение квантовой функции распределения 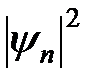 с классической функцией распределения для гармонического осциллятора
с классической функцией распределения для гармонического осциллятора 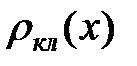
Контрольные вопросы
1. Сформулируйте постулаты квантовой механики и поясните их физический смысл?
2. Почему собственные функции эрмитового оператора могут служить базисом пространства Гильберта?
3. Какое свойство собственных функций эрмитового оператора обеспечивает разложение любой волновой функции по базису?
4. Как перейти от координатного представления волновой функции к F-представлению?
5. Поясните физический смысл коэффициентов разложения волновой функции по F- базису?
6. Принцип суперпозиции в квантовой механике и его физический смысл.
7. Физический смысл волновой функции. Кто впервые дал объяснение 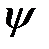 -функции?
-функции?
8. На каком основании волновую функцию можно рассматривать как вектор состояния в пространстве Гильберта? Кто впервые ввел такое представление?
9. Перечислите лауреатов Нобелевской премии, внесших существенный вклад в создание и развитие квантовой физики.
10. Условия полноты собственных функций операторов в квантовой механике.
11. Перечислите основные свойства волновых функций и операторов в квантовой механике.
12. Вывести условия, при которых две физических величины в квантовой механике имеют одновременно определенные значения.
13. Доказать, что если два оператора коммутируют, то они имеют одну систему собственных функций.
14. Почему в квантовой механике отсутствует понятие траектории и частицы?
15. Соотношение неопределенности Гейзенберга и его физический смысл.
16. При каких условиях две физические величины являются канонически сопряженными?
17. Вывести соотношение для физических величин, операторы которых не коммутируют.
18. Вывести явный вид собственных функций оператора импульса, нормированных на ящик (трехмерный случай).
19. Решить уравнение Шрёдингера для свободно движущейся частицы. Какие величины имеют определенное значение в этом состоянии?
20. Доказать эрмитовость оператора импульса.
21. Доказать эрмитовость оператора Гамильтона.
22. При каких условиях физическая величина в квантовой механике является интегралом движения?
23. Какое уравнение в квантовой механике позволяет анализировать интегралы движения?
24. Перечислите важнейшие законы сохранения и поясните их связь со свойствами симметрии пространства и времени.
25. Вывести закон сохранения энергии из свойства однородности времени.
26. Вывести закон сохранения импульса из свойства однородности пространства.
27. Вывести закон сохранения углового момента из свойства однородности и изотропности пространства.
28. Вывести уравнение, описывающее стационарное состояние квантовой системы?
29. Докажите, что стационарные состояния ортонормированны.
30. Вывести соотношения между средними значениями импульса и координаты частицы в состоянии y.
31. Вывести соотношение между средним значением силы и средним значением потенциальной энергии.
32. Исходя из соотношения неопределенностей оценить энергию основного состояния электрона в бесконечно глубокой потенциальной яме шириной 0.2 нм.
33. Решить уравнение Шрёдингера для частицы, движущейся в однородном потенциальном поле U=const.
34. Вычислить волновые функции состояний, в которых одновременно имеют определенные значения энергия и импульс частицы.
35. Вычислить волновой вектор и длину волны де Бройля в третьем возбужденном состоянии в бесконечно глубокой прямоугольной потенциальной яме.
36. Какова вероятность обнаружить электрон в первой трети бесконечно глубокой прямоугольной потенциальной ямы? Положить, что электрон находится в основном состоянии.
37. Электрон находится в одномерной бесконечно глубокой потенциальной яме шириной 0.1 нм. Найти плотность энергетических уровней dn/dE (число уровней на единичный интервал энергий).
38. Исходя из соотношения неопределенностей, оценить скорость движения электрона в атоме водорода. Размер атома принять 0.1 нм.
39. Доказать, что электрон не может находиться в атомном ядре. Размер ядра принять 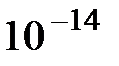 м.
м.
40. Вычислить наименьшее значение энергии нейтрона, заключенного в потенциальный ящик с абсолютно непроницаемыми стенками, расстояние между которыми 10-14м.
41. Для частицы в основном состоянии в одномерной прямоугольной потенциальной яме с абсолютно непрозрачными стенками вычислить среднее значения координаты и импульса частицы.
42. Вычислить неопределенность координаты в основном состоянии частицы в бесконечно глубокой потенциальной яме шириной a.
43. Вычислить неопределенность импульса в основном состоянии частицы в бесконечно глубокой потенциальной яме шириной a.
44. Проверить соотношение неопределенности для частицы в основном состоянии в бесконечно глубокой потенциальной яме.
45. Для линейного гармонического осциллятора, находящегося в основном состоянии вычислить <x2> и среднюю потенциальную энергию.
46. Для линейного гармонического осциллятора, энергия которого 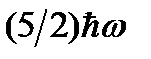 , вычислить среднюю кинетическую энергию.
, вычислить среднюю кинетическую энергию.
47. Почему любую физическую систему вблизи положения равновесия можно моделировать гармоническим осциллятором?
48. Дайте определение гармонического и ангармонического приближения.
Вычислить коэффициент прозрачности D барьера прямоугольной формы при U=20 эВ и a =0.1 нм для электрона и протона с энергией 10 эВ.
Для частицы массой m и энергией E<U0 найти коэффициент прозрачности барьера, заданного на потенциальной кривой: U (x) =U 0(1 -x 2/ a 2).
49. Какая доля электронов с энергией 1эВ пройдет через потенциальный барьер высотой 8 эВ и толщиной 0.5 и 0.3 нм?
50. Поток электронов с энергией 1 эВ движется к потенциальному прямоугольному барьеру высотой 10 эВ бесконечной ширины. На каком расстоянии от поверхности барьера плотность тока электронов уменьшится в e раз?
51. Чему равна вероятность нахождения электрона вне классических границ его движения для линейного осциллятора в первом возбужденном состоянии?
52. Приведите 10 примеров проявления туннельного эффекта в природе и технике.
53. Докажите тождество: [ 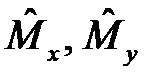 ]
] 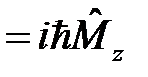 .
.
54. Докажите тождество: [ 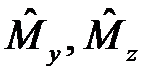 ]
] 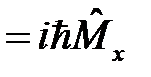 .
.
55. Докажите тождество: [ 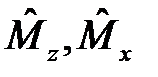 ]
] 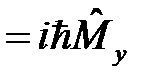 .
.
56. Докажите, что:[ 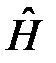 ,
, 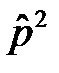 ]=
]= 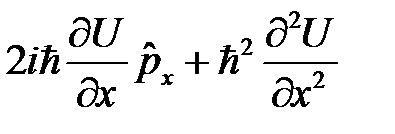 .
.
57. Докажите, что: [ 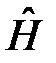 ,
, 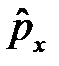 ]=
]= 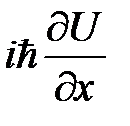 .
.
58. Докажите, что: [ 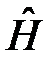 ,
, 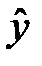 ]=
]= 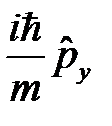 .
.
59. Найти собственные функции и собственные значения оператора 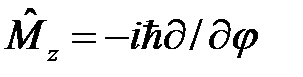 , j - азимутальный угол (учесть, что y(j)=y(j+2p)).
, j - азимутальный угол (учесть, что y(j)=y(j+2p)).
60. Найти собственные функции и собственные значения оператора 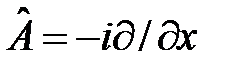 , если y(х)=y(х+a), где a =const.
, если y(х)=y(х+a), где a =const.
61. В одномерной прямоугольной бесконечно глубокой потенциальной яме шириной a находится частица в состоянии y(х)=Аsin2(pх/a). Определить вероятность пребывания частицы в основном состоянии и среднее значение кинетической энергии.
62. Определить среднее значение механической величины, описываемой оператором 
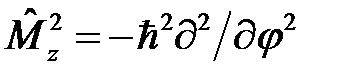 в состоянии y (j)= А sin2 j, где j - азимутальный угол (2p³ j ³0).
в состоянии y (j)= А sin2 j, где j - азимутальный угол (2p³ j ³0).
Литература
| 1. Шпольский Э. В. Атомная физика. Т. 2. М., Наука. 1984. | ||
| 2. Давыдов А. С. Квантовая механика. М., Наука. 1963. | ||
| 3. Блохинцев Д. И. Основы квантовой механики. М., Наука. 1983. | ||
| 4. Ландау Л. Д. Лившиц Е. М. Квантовая механика. М., Наука. 1989. | ||
| 5. Матвеев А.Н. Атомная физика. М., Высшая школа. 1989. 6. Балашов В.В., Долинов В.К. Курс квантовой механики. Ижевск. НИЦ «Регулярная и хаотическая динамика». 2001. 7. Галицкий В.М., Карнаков Б.М., Коган В.И. Задачи по квантовой механике. М., Наука. 1981. 8. Балашов В.В., Коренман Г.Я., Смирнов Ю.Ф., Юдин Н.П. Теоретический практикум по атомной и ядерной физике. Ч. 1. М., МГУ. 1980. 9. Флюгге З. Задачи по квантовой механике. Т. 1 и 2. М., Мир. 1974. |
Учебное издание
Шибков Александр Анатольевич
Основы Квантовой теории
Часть 1
Квантовая механика одномерного движения
Учебное пособие
Подписано в печать 26.01.2009 г. Формат 60´84/16. Бумага офсетная.
Гарнитура «Таймс». Усл. печ. л. 4,25. Уч.-изд. л. 4,54.
Тираж 100 экз. Заказ 1248.
Издательский дом ТГУ имени Г. Р. Державина
392008, г. Тамбов, ул. Советская, 190 г
Date: 2015-05-19; view: 2918; Нарушение авторских прав