Бесконечно глубокая яма

Важнейшими примерами движения частиц в потенциальных ямах является движение нуклонов в ядрах, электронов в атомах и молекулах. Основные закономерности финитного движения частиц можно исследовать на примере, когда форма потенциального рельефа имеет вид прямоугольной бесконечно глубокой ямы шириной а. На интервале (0, а) потенциальную энергию примем равной нулю, а вне этого интервала она обращается в бесконечность (Рис. 2.1). Вследствие этого частица при своём движении не может выйти за пределы отрезка (0, а) или, как говорят, частица находится в бесконечно глубокой потенциальной яме шириной а.

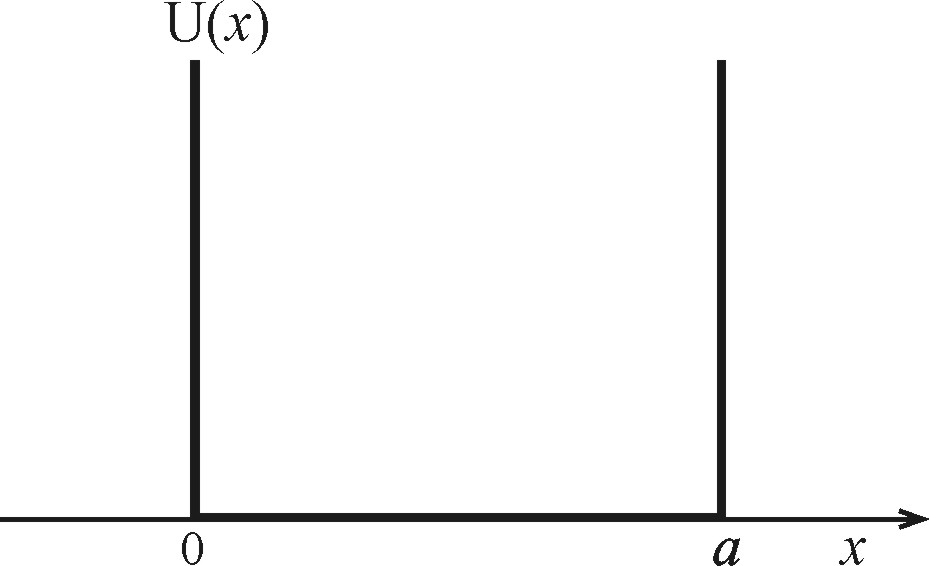
Рис. 2.1. Прямоугольная потенциальная яма бесконечной глубины

Поскольку вероятность нахождения частицы вне бесконечно глубокой потенциальной ямы равна нулю, то волновая функция вне интервала (0, а) равна нулю. Таким образом, получаем граничные условия для решения уравнения Шрёдингера:

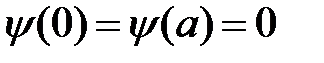. (1)

Поскольку потенциальная энергия U (x) не зависит от времени, то для вычисления волновых функций частицы необходимо решить стационарное одномерное уравнение Шрёдингера 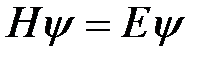с нулевым потенциалом на дне ямы, 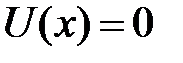, т.е.

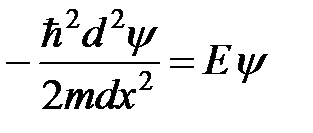. (2)

Приведём уравнение (2) к каноническому виду:

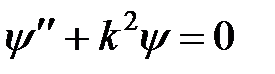, (3)

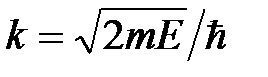где (4)

есть величина с размерностью волнового числа: м^{- 1}. Характеристическое уравнение: 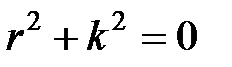имеет комплексные корни 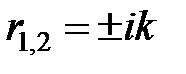. Общее решение дифференциального уравнения (3) запишем в виде

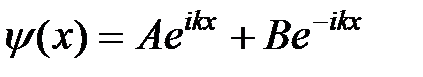. (5)

Стационарное уравнение Шредингера, как известно, содержит осциллирующий с частотой 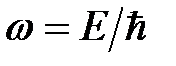временной множитель

. ()

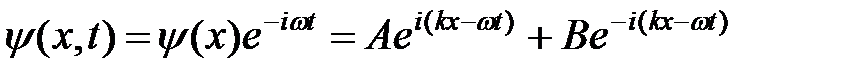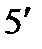Первое слагаемое представляет собой «падающую» волну де Бройля с амплитудой А, волновым числом 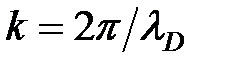и частотой 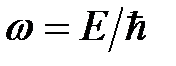, а второе слагаемое – «отражённую» волну де Бройля, т.е. волну, распространяющуюся в противоположном направлении. Эти волны когерентны, так как они имеют одинаковую длину волны 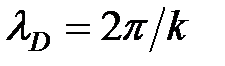. Обычно плоские волны де Бройля записывают без временного множителя, т.е. в виде (5).

Подставляя решение (5) в граничное условие 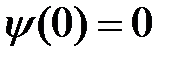, имеем 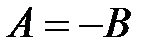и 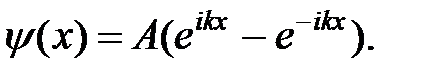Применяя формулу Эйлера 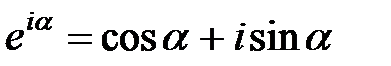, получим

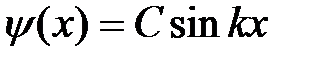, (6)

где 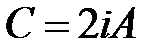– нормировочный множитель, который вычисляется из условия нормировки. Подставляя (6) в условие нормировки 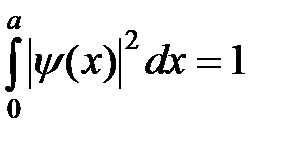, получим .

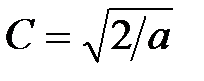Подставим теперь решение (6) во второе граничное условие: 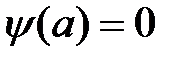и получим 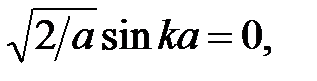откуда 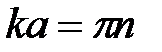, где n принимает натуральный ряд чисел 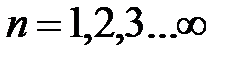. Таким образом, волновое число k – квантуется, т.е. принимает дискретный ряд значений

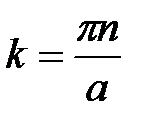. (7)

Подставляя (7) в (6) окончательно имеем для волновых функций, описывающих состояние частицы в бесконечно глубокой потенциальной яме шириной а:

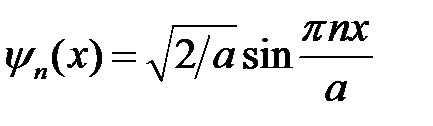. (8)

Для того, чтобы получить спектр энергии частицы, подставим найденные значения волновых чисел (7) в формулу (4):

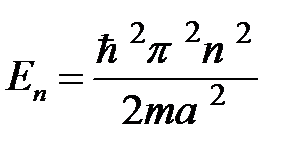. (9)

Как видно, решение (8) представляет стоячую волну де Бройля, которая образовалась в результате интерференции «падающей» и «отражённой» когерентных волн де Бройля, определяемых соотношением (5) или (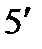). Условие образования стоячей волны (7) запишем в терминах длины волны де Бройля учитывая, что 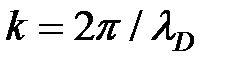, тогда получим

, ()

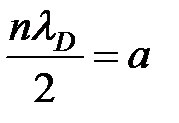т.е. стоячая волна образуется при условии, когда на ширине ямы укладывается целое число длин полуволн, равное квантовому числу n. Плотность вероятности, т.е. вероятность обнаружить частицу на единичном отрезке ямы, равна соответственно

. (10)

На рис. 2.2 представлены волновые функции частицы и соответствующие плотности вероятности первых состояний при n =1,2,3 и при n =20>>1.

Видно, что при небольших квантовых числах, распределение вероятностей для частицы в яме носит сильно нелинейный характер, но с ростом квантового числа функция плотности вероятности имеет тенденцию быть более однородной и в пределе больших квантовых чисел 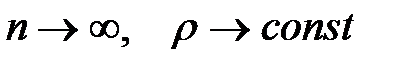, что соответствует предельному переходу к классической задаче. Действительно при больших квантовых числах n>> 1, длина волны частицы становится много меньше ширины ямы 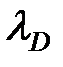<< а, что соответствует условию применимости классического описания, в котором волновые свойства частицы не учитываются. В тоже время квантовомеханическое описание используется в случае соизмеримости длины волны де Бройля частицы и характерного размера системы, ограничивающего движение частицы (ширины ямы), что соответствует случаю малых квантовых чисел.

а) б)

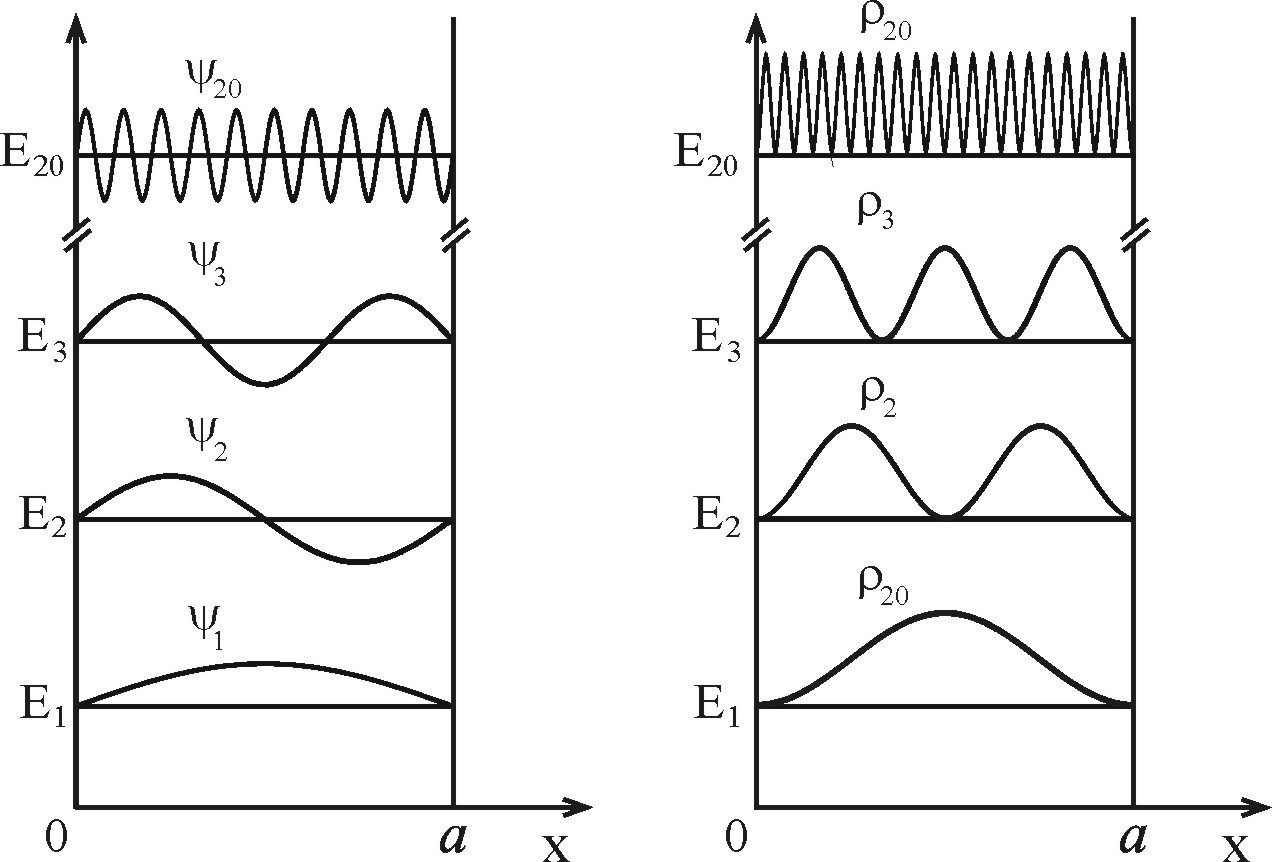
Рис. 2.2. Спектр энергии, волновые функции (а) и распределение плотности вероятности 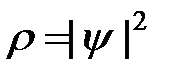(б) частицы в бесконечно глубокой прямоугольной потенциальной яме

Date: 2015-05-19; view: 754; Нарушение авторских прав