Квантовый гармонический осциллятор. Фононы

Так как потенциальная энергия осциллятора 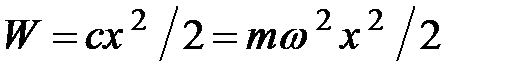не зависит от времени, то состояния осциллятора определяются стационарным уравнением Шрёдингера

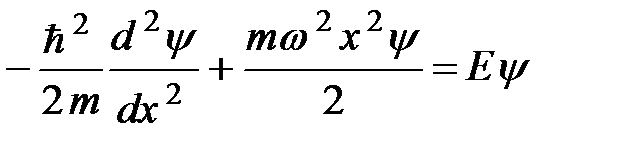. (2)

Для решения этого уравнения вводятся безразмерные величины

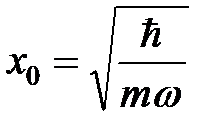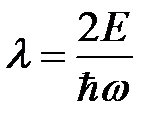, , . (3)

Обозначая дифференцирование по 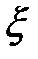штрихами и рассматривая 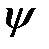как функцию 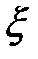, преобразуем (3) к виду

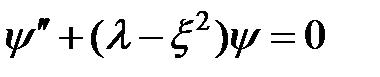. (4)

Непрерывные, однозначные и конечные решения этого уравнения существуют не при любых значениях 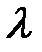, а только при 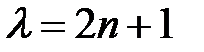, где 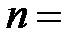0, 1, 2, 3.., а решения равны

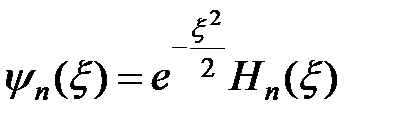, (5)

где 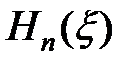– полином Чебышева-Эрмита, определяемый формулой

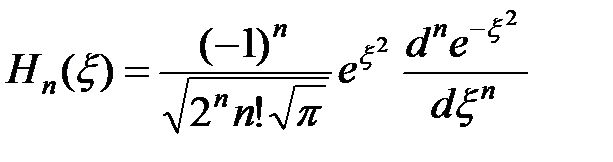, (6)

а соответствующий собственным функциям 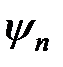спектр энергии осциллятора определяется выражением

. (7)

Таким образом, энергия гармонического осциллятора может принимать лишь дискретные значения. Число n, определяющее номер квантового уровня, называют главным квантовым числом. Положения первых уровней и вид потенциальной функции представлен на рис. 2.11.

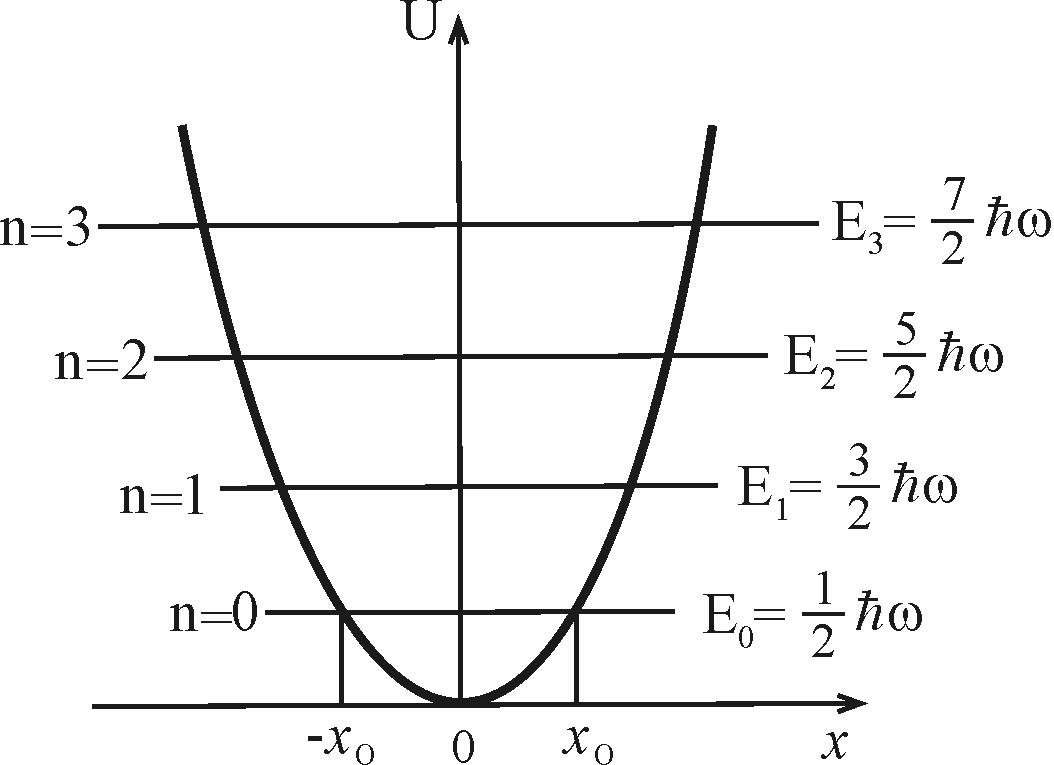
Рис. 2.11. Потенциальная энергия для осциллятора 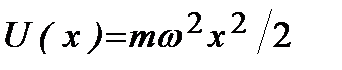и первые уровни энергии квантового гармонического осциллятора

Так как частица совершает финитное движение, её спектр энергии дискретен. Особенность движения частицы в параболической потенциальной яме состоит в том, что её спектр энергии, как видно из формулы (7) и рисунка, эквидистантен, т.е. расстояние между соседними уровнями не зависит от n и равно 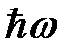. На этом основании можно ввести понятие элементарного возбуждения одномерного гармонического осциллятора, называемого фононом, с энергией 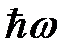. В основном, т.е. невозбужденном состоянии осциллятора число фононов равно нулю, в первом возбужденном состоянии имеется один фонон и т.д. Таким образом, квантовое число n численно равно количеству фононов в данном состоянии осциллятора. Поэтому квантовый осциллятор возбуждается дискретно, поглощая одинаковые порции энергии, равные .

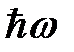Date: 2015-05-19; view: 1006; Нарушение авторских прав