Основное состояние частицы в бесконечной яме

Основное состояние квантовой системы это состояние с наименьшей энергией, т.е. состояние с n =1. Волновая функция основного состояния

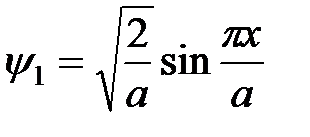
не имеет узлов, т.е. она не равна нулю ни в одной точке внутри ямы и равна нулю только на её границах 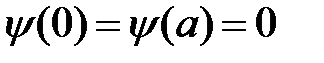. Отсутствие узлов волновой функции основного состояния является общим свойством квантовых систем.

Энергия основного состояния

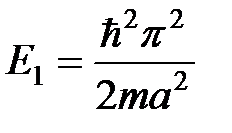
не равна нулю и возрастает при уменьшении размера ямы а. Таким образом, локализация частицы неизбежно сопровождается увеличением её энергии, что непосредственно вытекает из соотношения неопределённости Гейзенберга 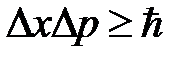: с уменьшением ширины ямы уменьшается неопределённость координаты частицы и соответственно растёт неопределённость её импульса, а так как средний импульс частицы в яме очевидно равен нулю, то это означает рост импульса частицы, а следовательно её полной энергии. Этот вывод также является общим свойством квантовых систем.

Перечислим основные свойства решений для частицы в яме, отличающие их от классической задачи.

1. Спектр энергии частицы в яме дискретный.

2. Распределение вероятности частицы в яме имеет вид стоячей волны, т.е. существенно отличается от равномерного распределения для классической задачи.

3. В отличие от классической частицы квантовая частица не может покоиться в яме в отсутствие внешних воздействий. Её минимальная энергия 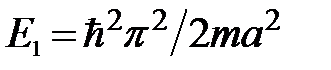связана с соотношением неопределённости Гейзенберга.

4. Квантовое число n, которое классифицирует собственные функции и спектр энергии частицы в яме, численно равно количеству узлов волновой функции, а также количеству полуволн де Бройля, которое укладывается на ширине ямы.

5. В пределе больших квантовых чисел 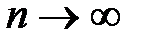квантовая задача переходит в классическую, так длина волны частицы оказывается много меньше ширины ямы 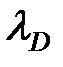<< a.

Date: 2015-05-19; view: 1254; Нарушение авторских прав