Частица в яме конечной глубины

Реальные системы частиц (ядра, атомы, молекулы и т.д.) представляют потенциальные ямы для составляющих их частиц (нуклонов и электронов) конечной глубины. Для исследования общих закономерностей движения частицы в таких системах рассмотрим одномерное движение частицы в яме шириной а, “левый берег” которой бесконечно высокий 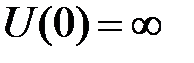, а “правый” имеет конечное значение при 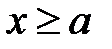, на дне ямы в интервале (0, а) положим 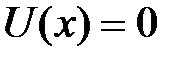(Рис. 2.3).

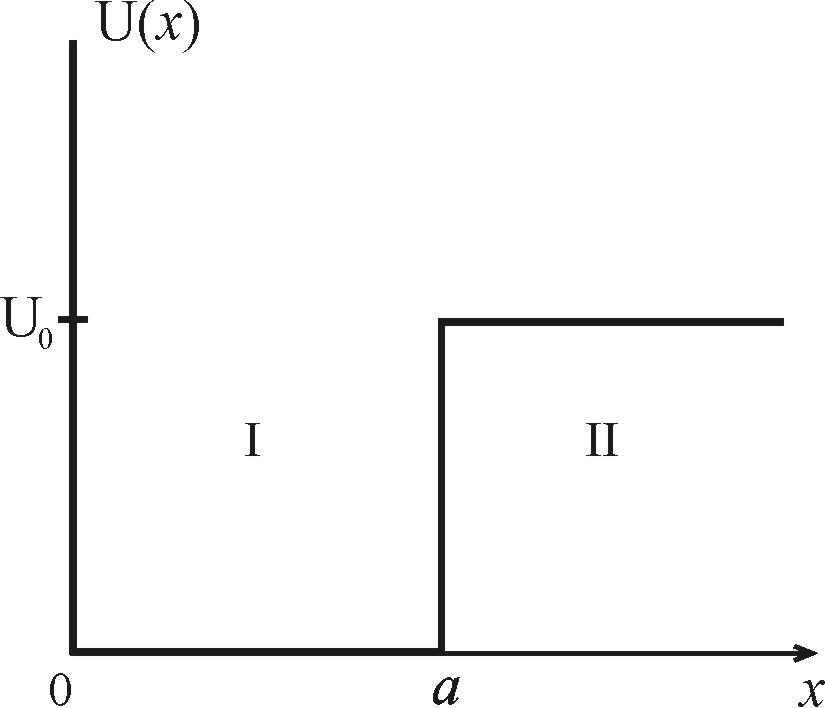
Рис. 2.3. Потенциальная яма конечной глубины

Так как в отрицательной области координаты x потенциальная энергия частицы бесконечна, то вероятность обнаружить частицу в этой области равна нулю 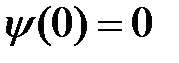. Задача сводится к решению стационарного уравнения Шрёдингера 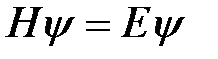в области I, т.е. в интервале (0, а) и в области II, т.е. при 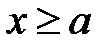, а затем к сшиванию полученных решений и их производных на границе x=a, т.е. 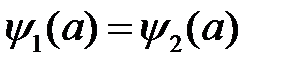и .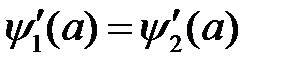

Область I, .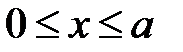

Запишем уравнение Шредингера, учитывая, что в области I U =0

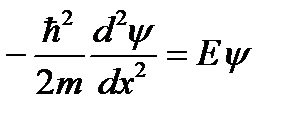. (1)

Приведём к каноническому виду:

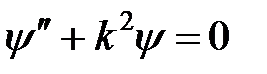, (2)

где 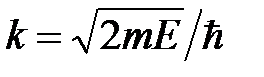– волновое число стоячей волны де Бройля.

Так как решения характеристического уравнения 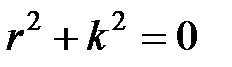комплексные 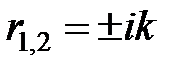, запишем решение дифференциального уравнения (2) в тригонометрической форме

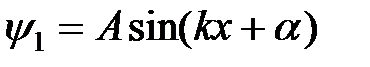, (3)

где А и – постоянные интегрирования. Подставляя (3) в граничное условие 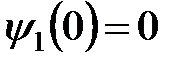, получим 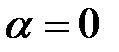и окончательно запишем решение для области I:

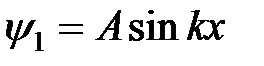. (4)

Область II, .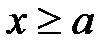

В области II потенциальная энергия частицы постоянна U=U ₀, поэтому возможны две ситуации а) энергия частицы E<U ₀; б) энергия частицы E>U ₀; этот случай соответствует движению частицы над ямой.

А. Рассмотрим первый случай, т.е E<U ₀. Запишем уравнение Шрёдингера

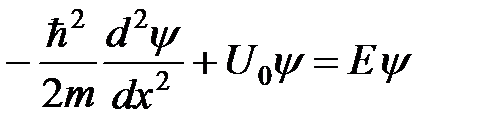. (5)

Приведём его к каноническому виду:

,

где 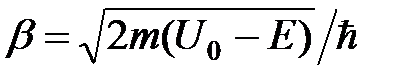. (6)

Характеристическое уравнение 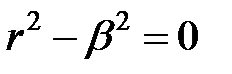имеет действительные корни 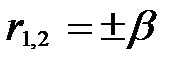поэтому решение (6) в отличие от решения для области I можно представить в виде суммы экспоненциальных функций

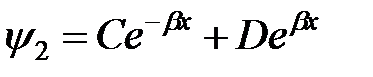. (7)

Так как волновая функция везде должна быть конечной, а 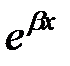при 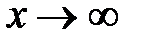неограниченно возрастает, то константу D необходимо положить равной нулю. Окончательно для второй области при E<U ₀ имеем:

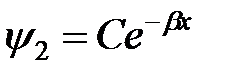. (8)

Для расчета спектра энергии, как и в яме бесконечной глубины необходимо использовать граничные условия. На “левой” границе ямы 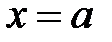, сошьём решения 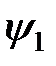и и 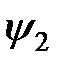их производные.

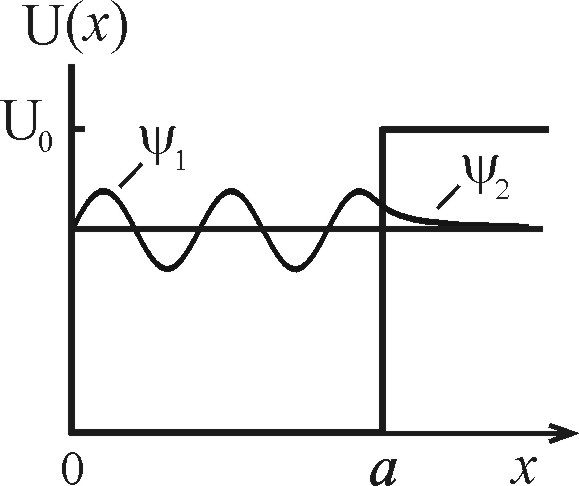
Рис. 2.4. Сшивание решени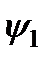й и 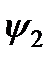на границе ямы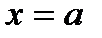

Граничные условия при :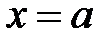

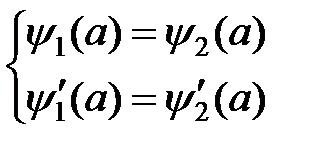
Подставим функции (4) и (8) в граничные условия:

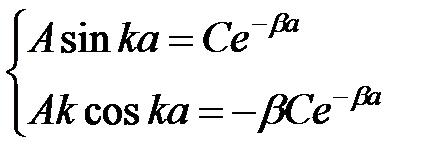
Поделив первое уравнение системы на второе, получим

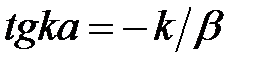. (9)

Для графического решения этого трансцендентного уравнения удобно сделать следующие преобразования: возведем (9) в квадрат и, учитывая, что 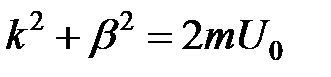, имеем

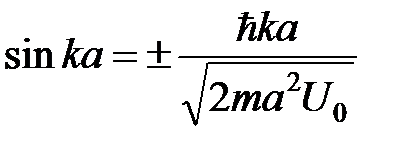. (10)

В качестве решений уравнения (10) берутся не все пересечения прямых 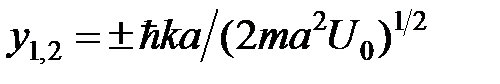с синусоидой , а лишь те, которые согласуются со знаком в уравнении (10), т.е. точки пересечения в чётных четвертях (Рис. 2.5). Так как число таких пересечений конечно 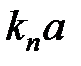, то им соответствует конечное количество уровней энергии

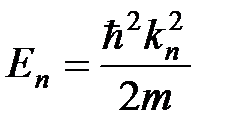. (11)

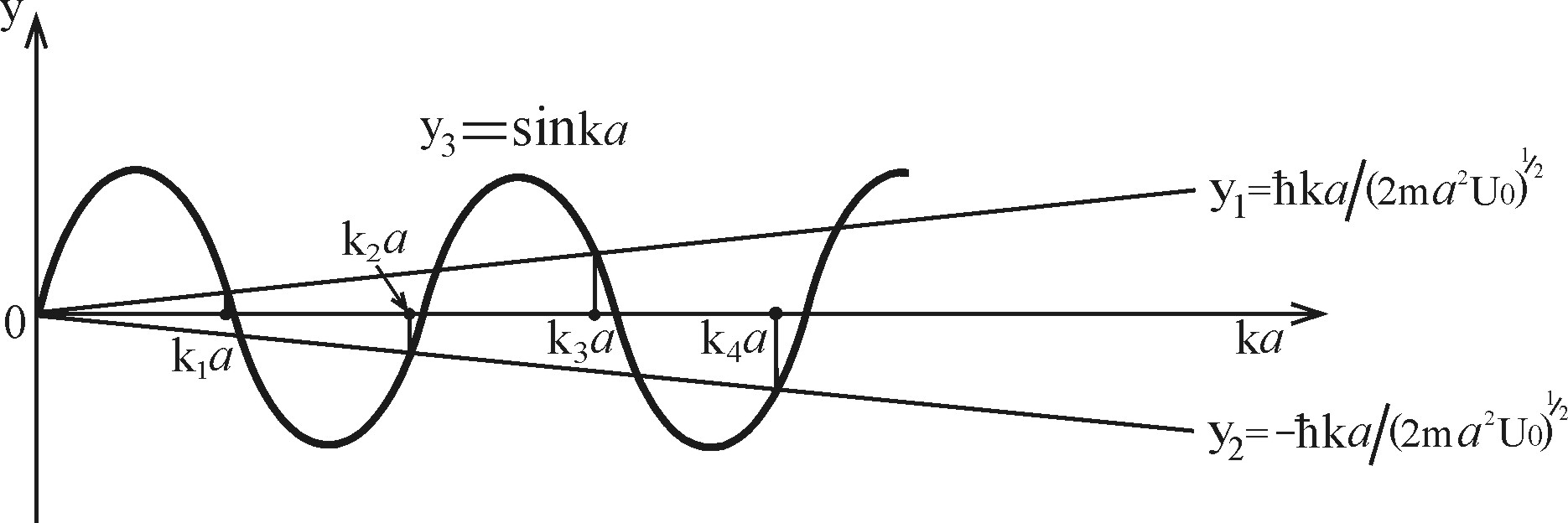
Рис. 2.5. Схема, поясняющая графическое решение уравнения (10)

Таким образом, в отличие от бесконечной ямы в потенциальной яме конечной глубины количество собственных значений энергии конечно. С уменьшением глубины ямы будет расти угол наклона прямых 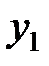и 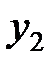и уменьшатся количество уровней. Когда этот угол превысит значение больше 45º, количество пересечений обратится в ноль. Таким образом, существует минимальная глубина ямы, при которой не происходит захвата частицы. Минимальную глубину ямы можно вычислить из очевидного условия

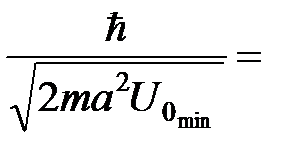tg45º=1, (12)

откуда получим: 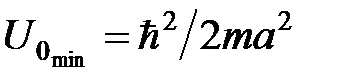. Существование минимальной глубины ямы связано с соотношением неопределённости и поэтому является общим свойством квантовых систем. Действительно, полагая неопределённость координаты 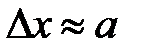,из соотношения неопределённости 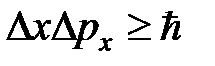получим 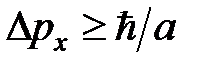и оценку энергии частицы: .

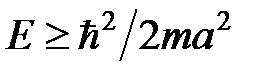Другое важное отличие от решения для бесконечно глубокой ямы является отличная от нуля вероятность обнаружить частицу за пределами ямы, то есть в области II, где классическая частица находится не может, так как ее потенциальная энергия была бы больше полной, кинетическая энергия – отрицательной, а скорость – мнимой величиной. Точки пересечения полной и потенциальной энергии 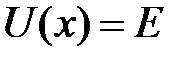называют «классическими точками поворота». Плотность вероятности 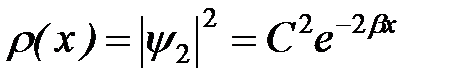убывает экспоненциально за классической точкой поворота 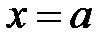. На расстоянии 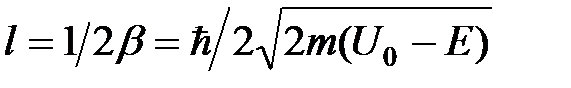функция плотности вероятности убывает в e раз. При увеличении глубины ямы 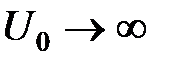глубина “просачивания” частицы в область II стремится к нулю: 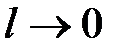, что совпадает с решением для движения частицы в бесконечно глубокой потенциальной яме.

Б. Рассмотрим случай, когда энергия частицы больше глубины ямы, то есть E>U ₀, частица движется над ямой. Тогда в области II форма уравнения (5) принимает вид

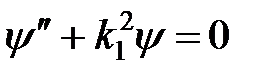, (13)

где .

Решение (13) запишем в виде

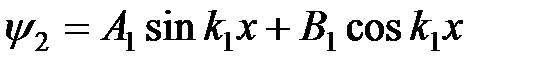. (14)

Сшивая на границе x=a решения для первой (4) и второй области при 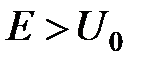(14), получим:

(15)

Решение системы (15) дают следующие соотношения между коэффициентами:

, .

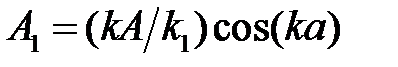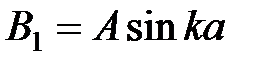Эти условия могут быть всегда удовлетворены. Поэтому в случае E>U ₀ спектр энергии частицы непрерывен; частица при своем движении не локализована в конечной области, ее движение инфинитно.

При движении над ямой на границе x=a скачком уменьшается волновое число. Соответственно длина волны де Бройля частицы скачком увеличивается в 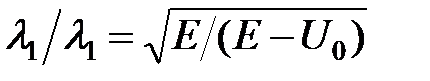раз.

Перечислим основные отличия для частицы в яме конечной глубины от решения для случая бесконечно глубокой ямы:

1. Спектр энергии частицы в яме дискретный, но состоит из конечного числа уровней.

2. Существует отличная от нуля вероятность обнаружить частицу за пределами ямы, т.е. в области, где E<U ₀ .

3. Существует минимальная глубина ямы, при которой не происходит локализация частицы в яме.

4. При движении частицы над ямой, т.е. при E>U ₀ спектр энергии непрерывен, а на границе x=a происходит скачок длины волны частицы.

Из анализа одномерного движения частицы в потенциальной яме следует важный вывод: если движение частицы финитно, то ее спектр энергии дискретный, если движение частицы инфинитно, то спектр энергии непрерывный.

Date: 2015-05-19; view: 2553; Нарушение авторских прав