Принцип Паули. Рассмотрим систему из двух слабо взаимодействующих фермионов

Рассмотрим систему из двух слабо взаимодействующих фермионов. Волновую функцию такой системы можно представить в виде произведения одночастичных состояний

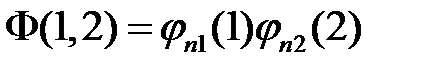, (1)

где n ₁ и n ₂ – совокупность квантовых чисел, характеризующих два различных квантовых состояния. Функция (1) является частным решением уравнения Шрёдингера. Другим частным решением уравнения Шрёдингера может быть функция

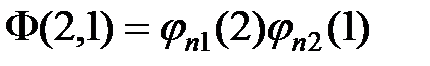, (2)

которая отличается от функции (1) перестановкой координат пары частиц относительно квантовых состояний n ₁ и n ₂.

Из принципа тождественности одинаковых частиц следует, что из функции (1) и (2) необходимо «сконструировать» линейные комбинации, обладающие требуемым свойством симметрии относительно перестановки координат пары частиц.

Для системы двух слабосвязанных фермионов, волновая функция системы должна быть антисимметричной

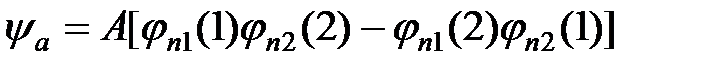, (3)

где константа 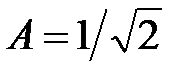находится из условия нормировки.

Очевидно функцию (3) можно представить в виде определителя:

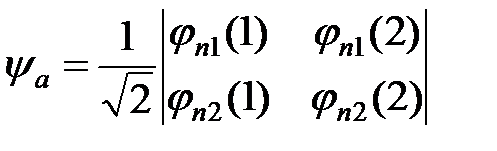, (4)

который называется определителем Слэтера.

Для системы из N слабо взаимодействующих фермионов определитель Слэтера имеет вид:

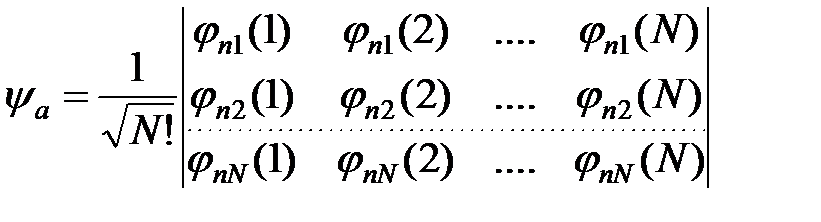. (5)

Если поменять местами (квантовыми состояниями) координаты любой пары частиц, то в определителе Слэтера (5) поменяются местами два столбца и определитель поменяет знак. Поэтому функция (5) является антисимметричной по отношению к перестановке координат любой пары частиц.

Если две частицы находятся в одинаковом квантовом состоянии, то это означает равенство строк определителя и определитель должен быть равен нулю, что означало бы отсутствие системы частиц. Отсюда следует принцип запрета Паули: в системе фермионов в одном квантовом состоянии может находиться не более одной частицы.

Date: 2015-05-19; view: 627; Нарушение авторских прав