Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Синглетное и триплетное состояния
|
|
Важным примером двухфермионной системы является система валентных электронов атомов, участвующих в образование молекул с ковалентной связью. Волновая функция системы зависит в общем случае от пространственных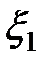 
, 
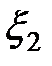и спиновых 
, 
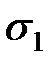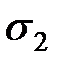координат фермионов, т.е.
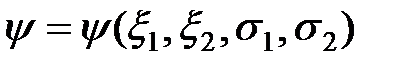. (1)
Если спин-орбитальное взаимодействие в системе пренебрежимо мало, то пространственные и спиновые переменные можно считать независимыми, а функцию (1) – представить в виде произведения координатной Ф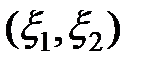 
и спиновой функции Х 
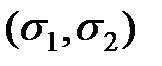, т.е.
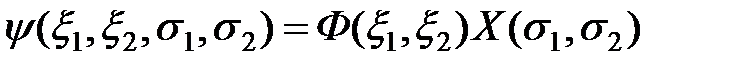. (2)
Для системы фермионов волновая функция (2) должна быть антисимметричной относительно перестановки координат (пространственных и спиновых). Это означает, что сомножители Ф и Х должны обладать противоположным свойством симметрии. Если координатная волновая функция симметричная (Фs), то спиновая должна быть антисимметричной (Ха). Антисимметричные спиновые функции обозначают с помощью схемы Юнга. Для системы из двух электронов суммарный спин такого состояния равен нулю, т.е.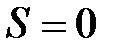 
, а мультиплетность (число возможных спиновых состояний) 
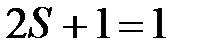. Такое состояние называют синглетным. Если координатная волновая функция антисимметрична (Фа), то спиновая должна быть симметричной (Хs), что соответствует схеме Юнга. Суммарный спин такого состояния 
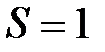, а мультиплетность 
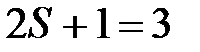. Такое состояние называют триплетным. Таким образом, возможны два физически различные состояния системы двух фермионов, которые описываются антисимметричными волновыми функциями:
триплетное: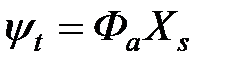 
,
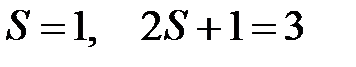синглетное: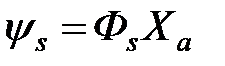 
.
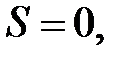
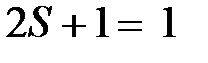Координатные функции Фа и Фs являются решением уравнения Шрёдингера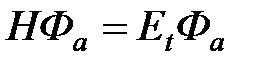 
и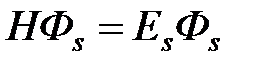 
, т.е. триплетному и синглетному состояниям системы двух фермионов (например, электронов) отвечают различные уровни энергии системы: Еt и Es.
Таким образом, полная энергия ферми-системы зависит от её полного спина. Можно говорить о некотором взаимодействии фермионов, приводящем к этой зависимости. Такое взаимодействие называют обменным. Для электронной системы обменное взаимодействие представляет часть кулоновского взаимодействия электронов, связанного с корреляцией их движения в соответствии с принципом Паули.
Date: 2015-05-19; view: 1128; Нарушение авторских прав