Классический гармонический осциллятор

Устойчивые физические системы (атомы, молекулы и т.д.) характеризуются наличием минимума (или минимумов) потенциальной энергии в точках пространства 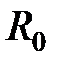, где 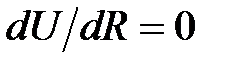. Разложим потенциальную энергию 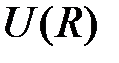вблизи положения равновесия 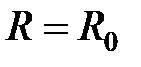в ряд Тейлора:

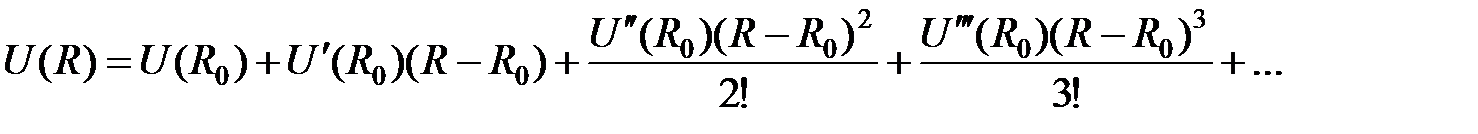
и ограничимся термом, содержащим вторую производную 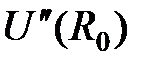. Такое приближение называют гармоническим. Учет более высоких членов разложения составляет ангармоническое приближение.

В гармоническом приближении потенциальную функцию можно заменить параболой 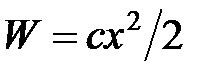, где 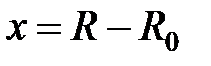– отклонение от положения равновесия, 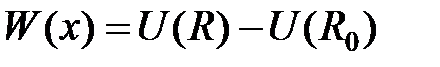– потенциальная энергия, отсчитанная от минимального значения (в положении равновесия), и .Сила, действующая в системе вблизи положения равновесия 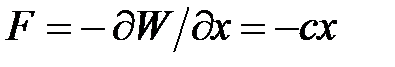, есть квазиупругая сила, поэтому решение уравнения динамики 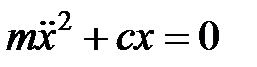дает гармонический закон движения 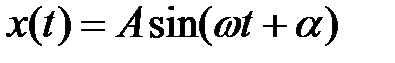, где 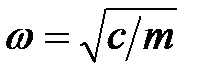– частота колебания.

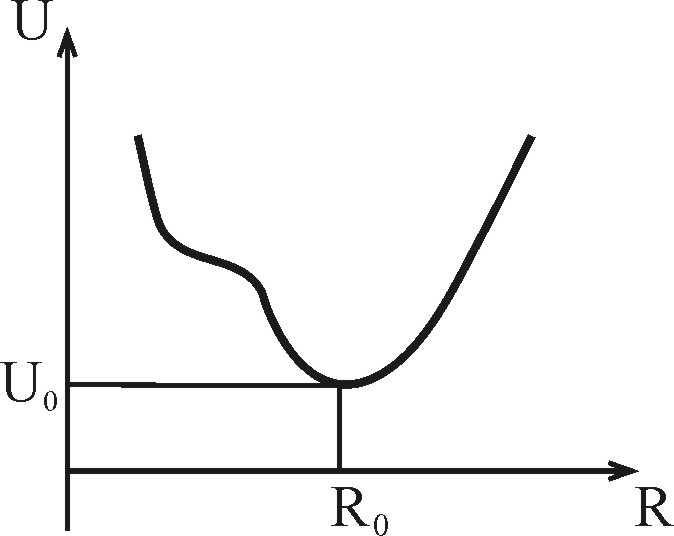
Рис. 2.10. Потенциальная функция устойчивой системы

Таким образом, гармонический осциллятор есть частица (или система частиц), которая движется в параболической потенциальной яме. Гармонические осцилляторы играют большую роль при исследовании малых колебаний систем около положения равновесия, в частности, колебаний атомов в молекулах, кристаллах и т.д.

Так как в квантовом пределе рассчитываются плотности вероятности 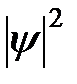, то для сравнения с классической задачей вычислим сначала распределение вероятности для одномерного классического осциллятора. Вычислим вероятность 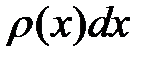обнаружить частицу в интервале от 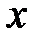до 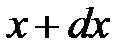. Эта вероятность пропорциональна времени 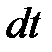, в течение которого частица проходит отрезок 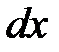. Если период колебаний есть , то можно положить

,

где 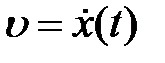– скорость частицы.

Так как для классического гармонического осциллятора закон движения есть 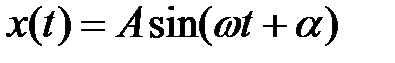, то скорость 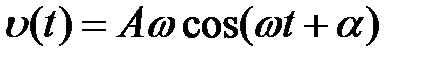, где 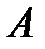– амплитуда колебаний, 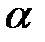– начальная фаза. Выражая скорость 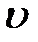через координату 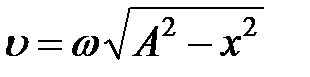, получим для классической плотности вероятности

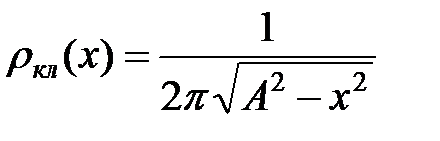. (1)

Date: 2015-05-19; view: 621; Нарушение авторских прав