Перестановочная симметрия. Бозоны и фермионы

В классической механике состояние частицы задаётся обобщёнными координатами и обобщёнными импульсами. С течением времени их значения непрерывно изменяются и частица описывает траекторию в конфигурационном и в фазовом пространстве. В квантовой механике из-за соотношения неопределённости Гейзенберга 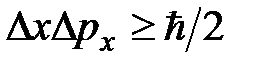состояние частицы нельзя описать с помощью траектории вследствие одновременной неизмеримости координаты и импульса частицы. Это приводит к неразличимости одинаковых частиц.

Рассмотрим систему, состоящую из N одинаковых частиц, например, электронную систему атома или молекулы. В момент времени t ₀ пронумеруем все электроны. Из-за отсутствия траектории электронов принципиально невозможно сохранить их нумерацию в будущий момент времени t. Поэтому в квантовой механике одинаковые частицы физически неразличимы. Это утверждение и составляет смысл принципа тождественности одинаковых частиц.

Для его количественного описания вводится оператор перестановки координат пары частиц:

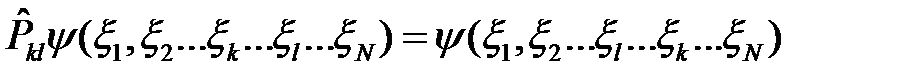. (1)

Из принципа тождественности одинаковых частиц следует, что перестановка координат пары частиц является преобразованием симметрии, поэтому оператор перестановки коммутирует с оператором Гамильтона системы 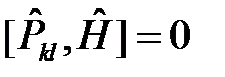, а собственные значения оператора перестановки являются интегралами движения.

Таким образом, перестановочная симметрия, связанная с принципом тождественности одинаковых частиц, приводит к чисто квантовому закону сохранения – сохранению собственных значений оператора перестановки координат пары частиц, – который не имеет аналога в классической механике.

Рассмотрим систему из двух одинаковых частиц. По определению, действие оператора перестановки состоит в следующем:

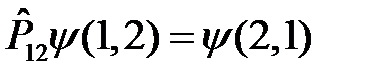. (2)

Собственные значения 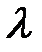оператора перестановки находятся из операторного уравнения

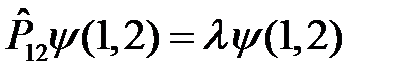. (3)

Подействуем слева на уравнения (2) и (3) оператором 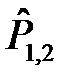и получим

,

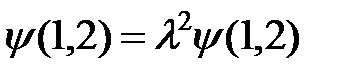откуда 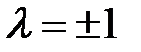(очевидно оператор перестановки эрмитов, поэтому его собственные значения действительны).

Существование двух противоположных по знаку собственных значений оператора перестановки приводит к двум различным видам волновых функций, описывающих системы одинаковых частиц: симметричных и антисимметричных.

Если функция не изменяет знака при перестановке координат пары частиц, т.е. :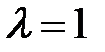

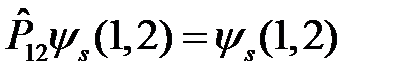, (4)

то она является симметричной относительно перестановки координат пары частиц, а если меняет знак, т.е. :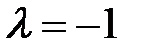

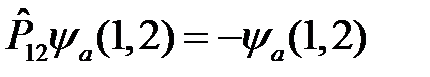, (5)

то волновая функция системы является антисимметричной относительно перестановки координат пары частиц.

Закон сохранения собственных значений оператора перестановки состоит в том, что если в данный момент времени состояние системы описывается симметричной (антисимметричной) волновой функцией, то это свойство симметрии состояния будет сохраняться сколь угодно долго.

Симметричные и антисимметричные волновые функции описывают системы, состоящие из двух различных сортов частиц: бозонов (частиц с целочисленным значением спинового числа) и фермионов (частиц с полуцелым спином) соответственно.

Важнейшими примерами бозонов являются кванты физических полей – переносчиков фундаментальных взаимодействий – фотоны, гравитоны, глюоны, промежуточные бозоны, а также ядра с чётным количеством нуклонов и т.д. Примеры фермионов – кварки, нуклоны, электроны, ядра с нечётным числом нуклонов и т.д.

Системы из большого количества одинаковых частиц, бозонов и фермионов, подчиняются различным квантовым статистическим распределениям частиц по энергиям, Бозе-Эйнштейна или Ферми-Дирака соответственно, и обладают совершенно различными физическими свойствами. Принцип тождественности одинаковых частиц налагает определённые ограничения на принцип суперпозиции состояний: физический смысл имеют лишь такие линейные комбинации состояний, которые обладают необходимым (для данного сорта частиц) свойством симметрии относительно перестановки координат любой пары частиц.

Date: 2015-05-19; view: 694; Нарушение авторских прав