Теоремы Эренфеста

В квантовой механике координаты и импульсы частицы одновременно неизмеримы, что следует из соотношения неопределённости Гейзенберга 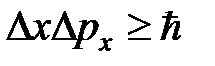, но между квантовомеханическими средними значениями этих величин соблюдаются соотношения классической механики, например, 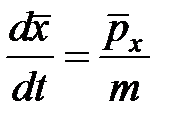. Подобного рода соотношения непосредственно следуют из анализа уравнения движения в форме Гейзенберга для операторов координаты и импульса и выражается в виде теорем Эренфеста.

Теорема I

В качестве оператора в уравнении движения Гейзенберга

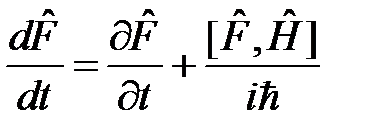(1)

рассмотрим оператор координаты, т.е. 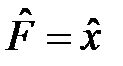. Очевидно, 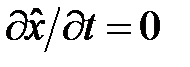и так как оператор умножения 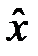очевидно коммутирует с оператором умножения – оператором потенциальной энергии 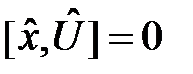, то

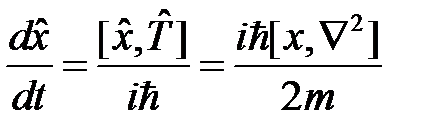, (2)

где 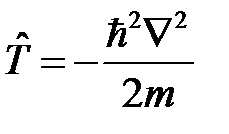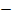оператор кинетической энергии.

Вычислим коммутатор 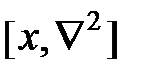. Для этого подействуем им слева на пробную функцию 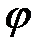(x, y, z): .

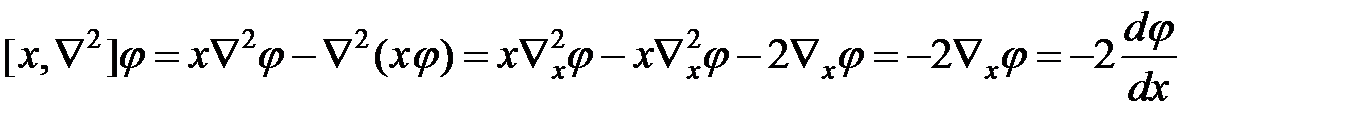(Здесь мы использовали формулу для второй производной произведения двух функций 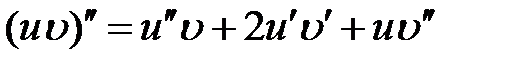). Таким образом, коммутатор 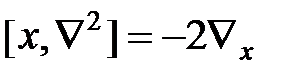. Подставляя в (2), получим

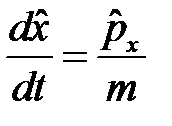. (3)

К квантовомеханическим средним значениям можно перейти с помощью формулы среднего (см. постулат соответствия)

.

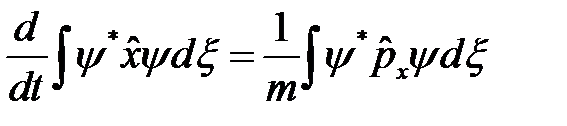Отсюда следует, что

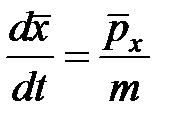. (4)

При движении частицы среднее значение координаты и импульса изменяются также как и в классической механике. Это утверждение и формула (4) выражает I-ая теорема Эренфеста.

Теорема II

В качестве оператора 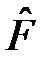в уравнении движения Гейзенберга (1) рассмотрим оператор импульса 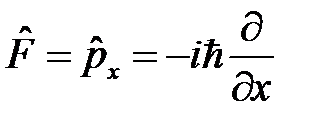. Очевидно 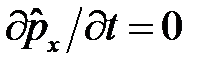. Так как оператор 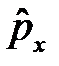коммутирует с операторами 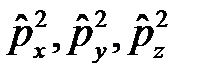и, следовательно, с оператором кинетической энергии 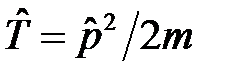, то

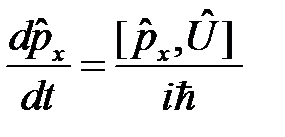. (5)

Вычислим коммутатор 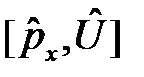. Для этого подействуем им слева на пробную функцию 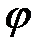(x, y, z):

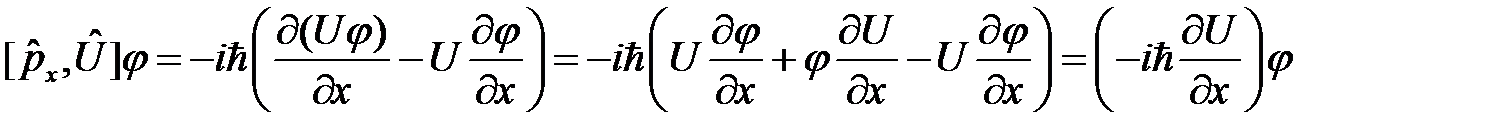. Подставляя в (5), получим:

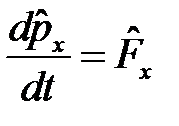, (6)

где 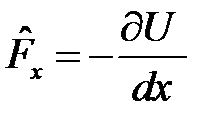– оператор проекции силы на ось х. Используем формулу среднего:

.

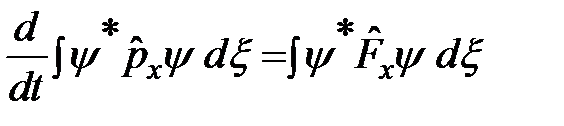Окончательно имеем:

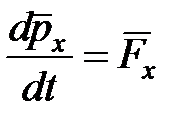. (7)

Производная по времени среднего импульса равна средней силе. Это утверждение выражает вторую теорему Эренфеста.

Дифференцируя (4) по времени и учитывая (7), получим:

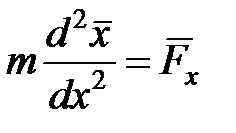. (8)

Из теорем Эренфеста следует, что средняя координата частицы и средняя сила в квантовой механике находятся в том же соотношении, в каком координата частицы и сила находятся в классической механике, т.е. связаны уравнениями движения Ньютона.

1.8. Канонически сопряжённые физические величины

Две физические величины 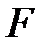и в одном и том же состоянии 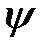могут иметь случайные значения или определённые значения в зависимости от коммутационных соотношений для операторов этих величин 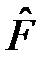и .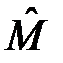

Если два оператора 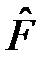и 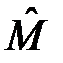не коммутируют, т.е. 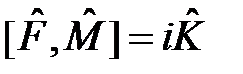, то для соответствующих им физических величин 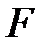и соблюдается соотношение неопределённостей:

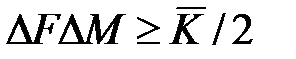, (1)

т.е. величины 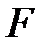и одновременно не измеримы в одном состоянии. Такие величины называются канонически сопряженными физическими величинами, а соотношение (1) - соотношением неопределенности для канонически сопряженных физических величин.

Здесь 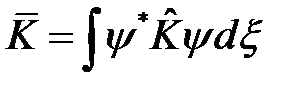; 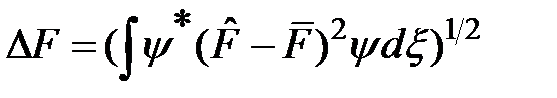и .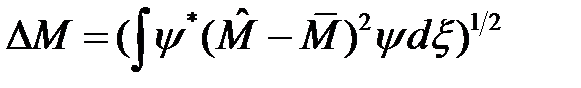

Из соотношения (1) можно получить соотношение неопределённости Гейзенберга, полагая 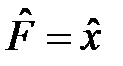, а . Для этого вычислим коммутатор

.

Согласно (1), получим:

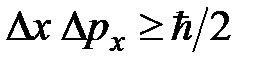. (2)

Таким образом, соотношение неопределённости Гейзенберга является частным случаем более общего соотношения неопределённостей для канонически сопряженных физических величин (1).

Если же два оператора 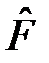и 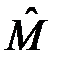коммутируют, т.е. 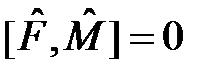, то они имеют одну общую систему собственных функций и, следовательно, соответствующие им физические величины F и M одновременно (в одном состоянии) имеют определённое значение. Докажем это утверждение.

Рассмотрим операторное уравнение с оператором :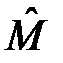

.

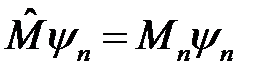Подействуем слева на это уравнение оператором :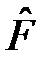

.

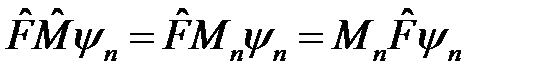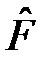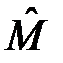Так как операторы и коммутируют, то 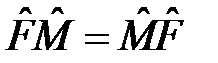. Делая замену, получим:

. (3)

Из (3) видно, что функция 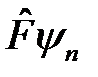с точностью до некоторой константы 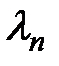есть собственная функция оператора 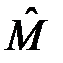, т.е. 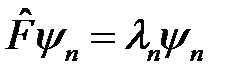. Таким образом, функции 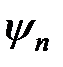являются собственными функциями двух операторов 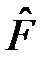и 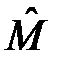, а их собственные значения 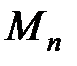и 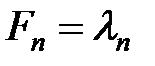одновременно имеют определённые значения в этих состояниях.

Date: 2015-05-19; view: 1868; Нарушение авторских прав