Закон сохранения углового момента

В классической механике закон сохранения углового момента выводится из свойства изотропности пространства. Это свойство означает инвариантность потенциальной функции относительно поворота на любой угол. Очевидно, однородное пространство 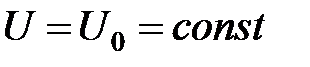обладает свойством изотропности. Другим важным примером изотропного пространства является потенциальная функция, обладающая свойством центральной симметрии 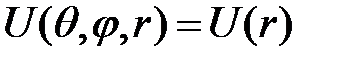, где 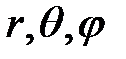– координаты частицы в сферической системе координат.

Запишем уравнение движения в форме Гейзенберга для оператора квадрата углового момента :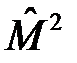

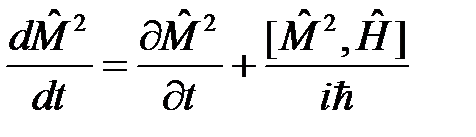. (13)

В сферической системе координат ,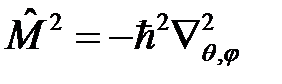

где 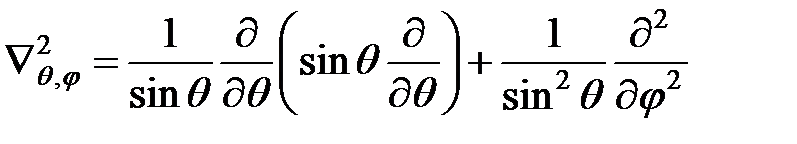– угловая часть оператора Лаплас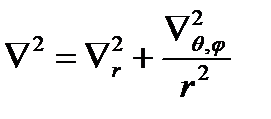а: , а 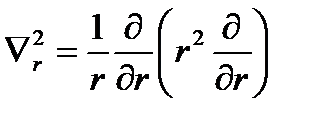– радиальная часть оператора Лапласа.

Оператор 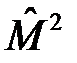не зависит явно от времени, поэтому 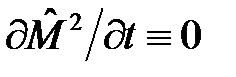. Для вычисления коммутатора 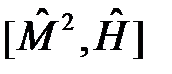запишем сначала оператор Гамильтона в сферической системе координат

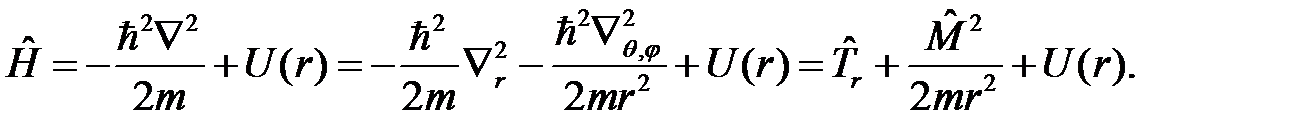
Здесь 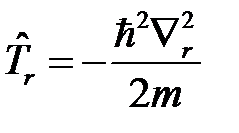– оператор кинетической энергии движения частицы по радиусу-вектору 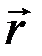, а оператор 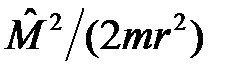– оператор трансверсального движения частицы.

Вычислим теперь коммутатор :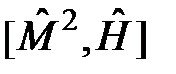

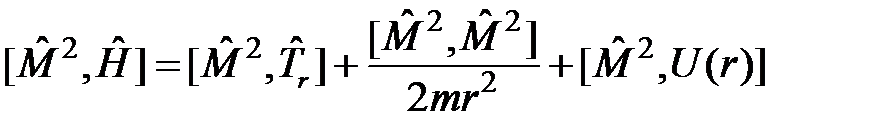. (14)

Так как оператор 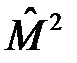действует на угловые координаты частицы 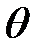и 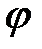, а оператор 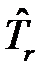и U(r) - на координату r, то первый и третий коммутаторы тождественно равны нулю, а второй коммутатор тривиально равен нулю, так как любой оператор коммутирует сам с собой: 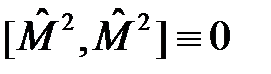. Поэтому 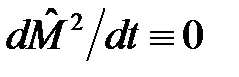и собственные значения оператора 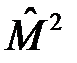, то есть 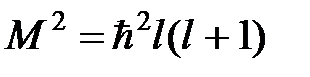являются интегралами движения, где l= 0,1,2,3 …∞, обозначают соответственно s, p, d, f… – состояния с определенным значением квадрата углового момента .

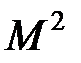Таким образом, если на частицу не действуют внешние силы или равнодействующая сил равна нулю, то U = U ₀ = const. В этом случае говорят, что пространство однородно и изотропно. Для частицы, которая движется в однородном пространстве сохраняются, кроме полной энергии 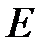, импульс 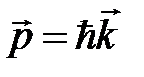и модуль вектора углового момента 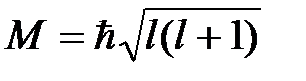. Так как оператор 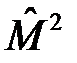коммутирует с оператором 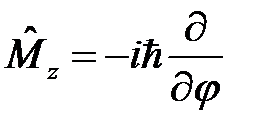, то в этой ситуации сохраняется еще и проекция углового момента на ось 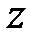, т.е. 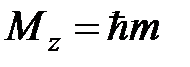, где m – магнитное квантовое число, которое принимает (2 l+ 1) различных значений от –l до +l через единицу.

Состояния с определенным значением 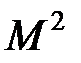есть собственные функции оператора 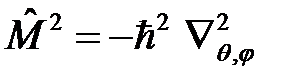, которые являются решением соответствующего операторного уравнения

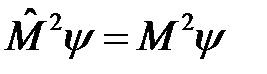. (15)

Решение уравнения (15) хорошо известно из курса математической физики. Это сферические (или шаровые) функции .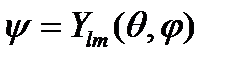

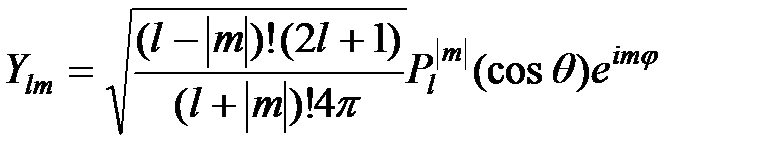
где 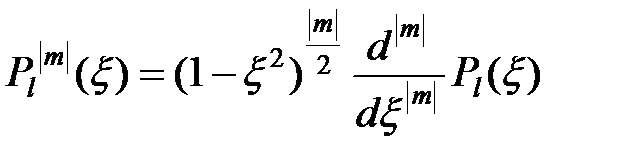– присоединенная функция Лежандра (здесь 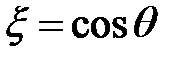) и

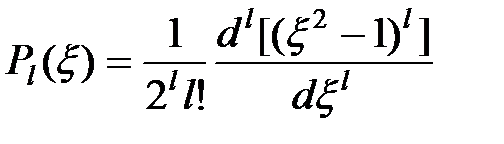– полином Лежандра,

где l= 0, 1, 2 …∞,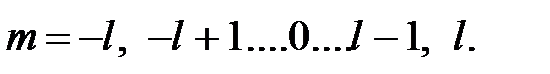

Состояние с определенным значением проекции углового момента на ось z есть решение соответствующего операторного уравнения 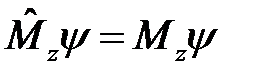, то есть

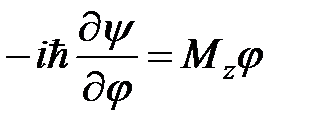. (16)

Его решения с учетом условия цикличности :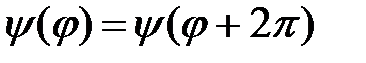

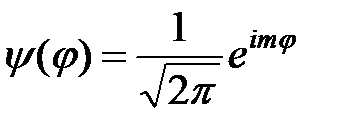(17)

интерпретируют как волны де Бройля, “бегущие по кругу”.

Здесь важно подчеркнуть полный набор коммутационных соотношений для оператора углового момента и его компонент:

,

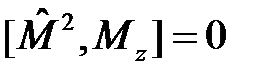
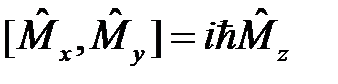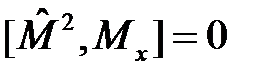
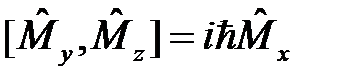, (18)

,

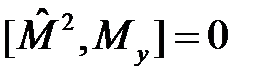
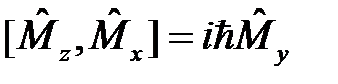Из этих коммутационных соотношений следует, что одновременно измеримы 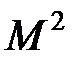и одна из проекций, например 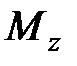, а проекции углового момента M_x, M_y, M_z одновременно неизмеримы. Это приводит к картине пространственного квантования углового момента.

Рассмотрим, для примера, d- состояние частицы в однородном или центрально-симметричном потенциальном поле. В этом состоянии l= 2, 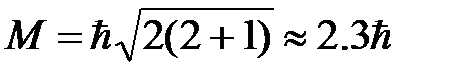, m = – 2, – 1, 0, +1, +2.

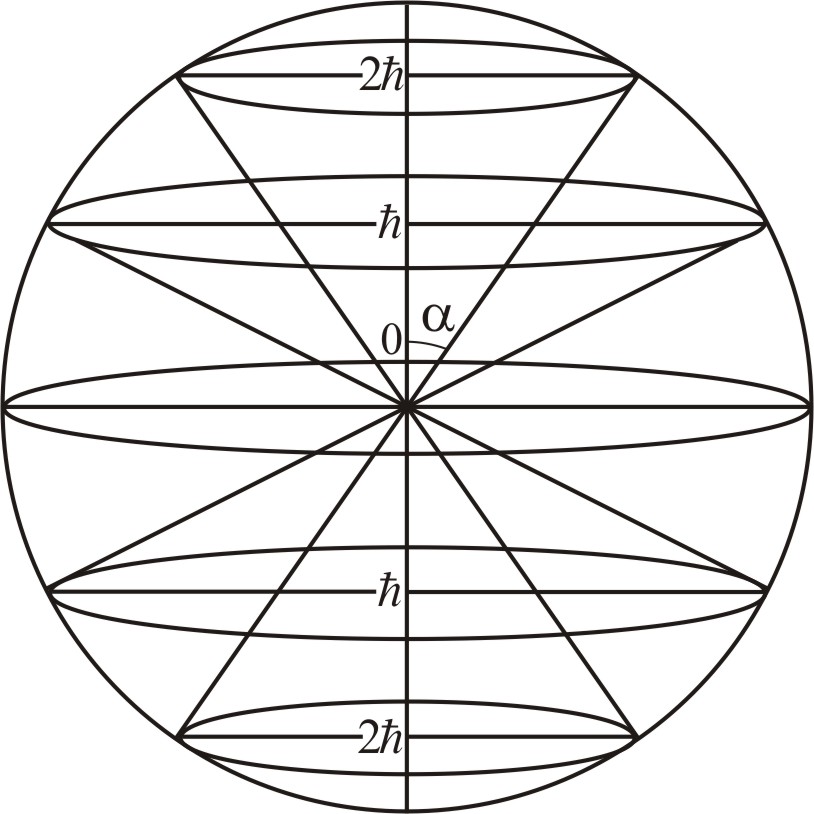
Рис. 1.1. Картина пространственного квантования углового момента в d -состоянии

Из рис. 1.1 видно, что вектор углового момента 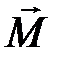находится на конусе с углом

:

.

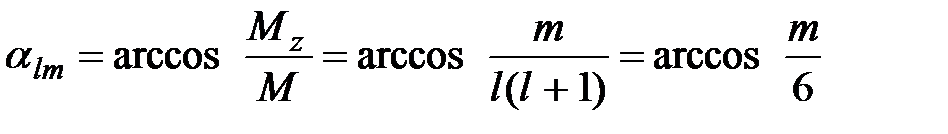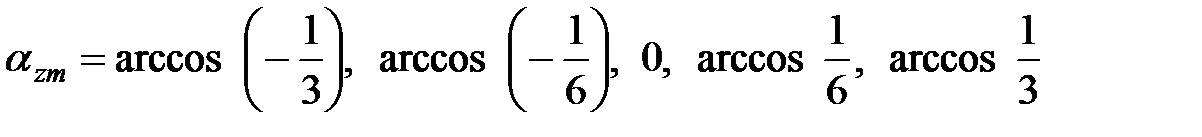Значение угла 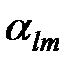, как видно из формулы квантуется, что и приводит к картине пространственного квантования углового момента.

Таким образом, в изотропном потенциальном поле состояние частицы характеризуется в общем случае тремя квантовыми числами:

n – главное квантовое число, которое классифицирует значение полной энергии частицы E_n;

l = 0, 1, 2, 3… – орбитальное квантовое число, которое определяет значение модуля углового момента ;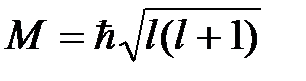

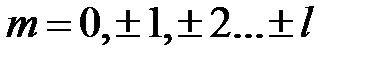– магнитное квантовое число, определяющее проекции углового момента на ось z: .

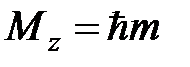Date: 2015-05-19; view: 1220; Нарушение авторских прав