Закон сохранения импульса

В классической механике закон сохранения импульса выводится из свойства однородности пространства, то есть из инвариантности потенциальной энергии системы по отношению к сдвигу (трансляции) на произвольный вектор. Очевидно, трансляционная симметрия однородного пространства означает, что в любой точке пространства потенциальная энергия одинакова U(x,y,z) = U₀ = const. Оператор Гамильтона в этом случае удобно представить в следующем виде 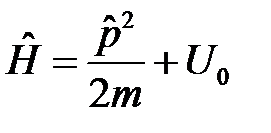. Запишем уравнение движения в форме Гейзенберга (5) для оператора импульса

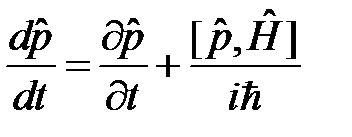. (7)

Так как 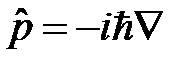, то очевидно 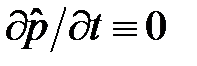. Коммутатор 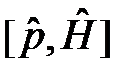в случае однородного пространства также тождественно равен нулю, так как

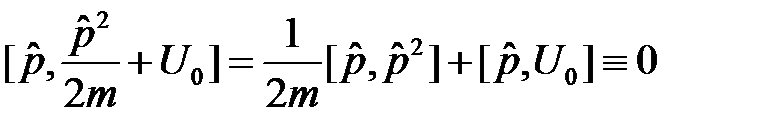. (8)

Поэтому получаем 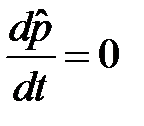и импульс частицы является интегралом движения, то есть сохраняется во времени. Соответствующие определенным значениям импульса состояния частицы являются собственными функциями оператора импульса. Их можно получить, решая операторное уравнение

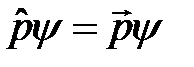. (9)

Спроектируем это уравнение на одну степень свободы, например, на ось х:

()

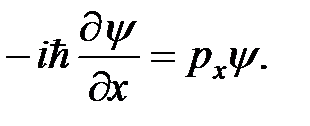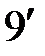Его решение: 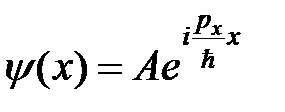имеет вид плоской волны де Бройля с амплитудой А и волновым числом 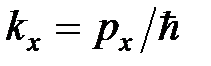. Постоянная интегрирования A находится из условия нормировки. Для нормировки функции такого вида применяют специальный метод, называемый “нормировкой на ящик”. Движение частицы рассматривается в потенциальном ящике, внутри которого потенциальная энергия постоянна U = U₀, а его размеры значительно превышают длину волны де Бройля частицы L_x >> λ_д. Тогда по условию нормировки

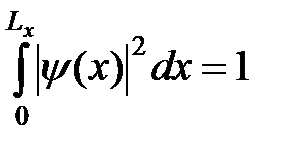. (10)

Подставляя в (10) решение 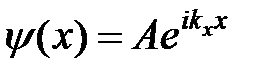, получим 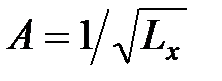, а для плотности вероятности 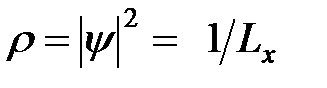. Таким образом, в состоянии с определенным значением импульса, плотность вероятности (вероятность обнаружить частицу в единице объема) не зависит от координат. Окончательно имеем:

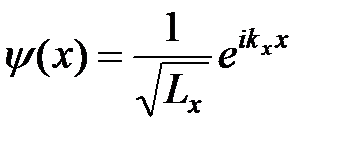. (11)

Волновую функцию состояния с определенным вектором импульса (9) можно получить, используя свойство мультипликативности волновой функции

,

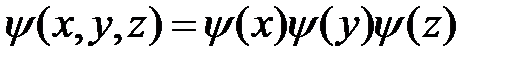которое непосредственно вытекает из теоремы о вычислении вероятностей независимых событий (движение частицы по x, y и z). Тогда собственную функцию оператора импульса (решение уравнения (9)) можно записать в виде

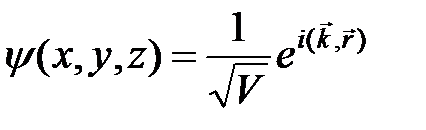, (12)

где 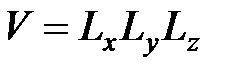– объем пространства (ящика), в котором движется частица, 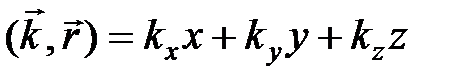– скалярное произведение волнового вектора 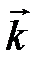и радиуса вектора 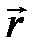частицы.

Таким образом, состояние 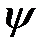с определенным импульсом 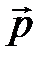есть плоская волна де Бройля (12) с амплитудой, равной 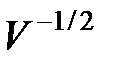и длиной волны де Бройля 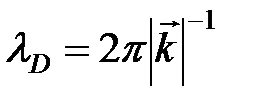. С другой стороны, результирующая сила, действующая на частицу, связана с потенциальным рельефом как 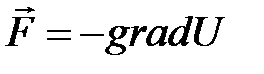. Для постоянной потенциальной функции 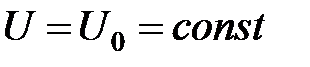сила 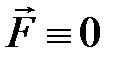и плоская волна де Бройля (12) описывает состояние свободно движущейся частицы. Таким образом, как в классической, так и в квантовой механике, состояние свободного движения частицы есть состояние с определенным значением импульса.

Date: 2015-05-19; view: 572; Нарушение авторских прав