Уравнение непрерывности в квантовой механике

Одним из основных уравнений классической электродинамики и механики сплошных сред является уравнение непрерывности

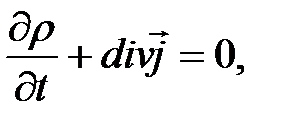(1)

которое выражает законы сохранения заряда и массы соответственно. В случае электродинамик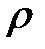и и – плотность заряда и плотность электрического тока, а в случае механики сплошных сред 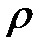и – массовая плотность среды и плотность потока массы соответственно.

В квантовой механике состояние системы описывается нормированной волновой функцией: с течением времени состояние системы может измениться, но неизменным остается условие нормировки. Таким образом, в соответствии с постулатом состояния должен соблюдаться закон сохранения условия нормировки волновой функции:

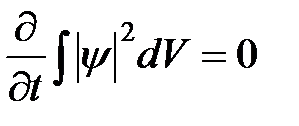. (2)

Это условие приводит к уравнению непрерывности в квантовой механике. Для его вывода запишем уравнение Шредингера и уравнение, ему комплексно сопряженное:

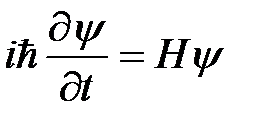
Умножим слева первое уравнение на 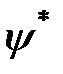, а второе – на 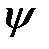и, вычитая второе из первого, получим

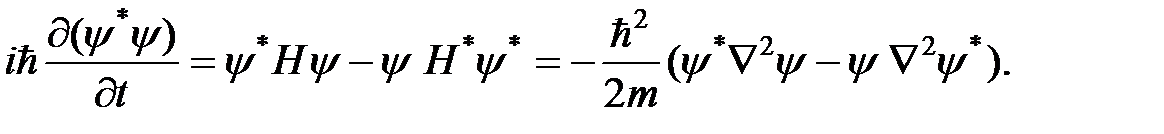
Применяя известную формулу векторного анализа 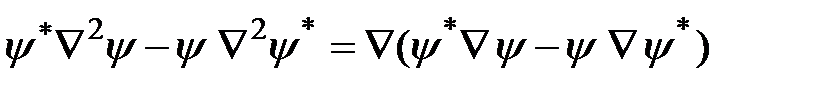, имеем:

.

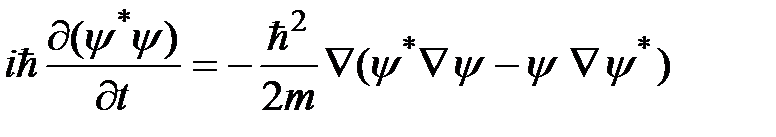В соответствии с постулатом состояния есть плотность вероятности . Вводя далее вектор плотности потока вероятности

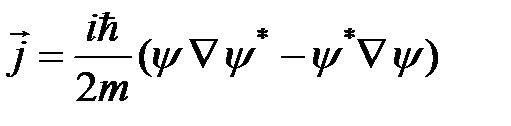, (3)

получим уравнение непрерывности в квантовой механике

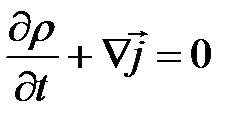. (4)

Умножая вектор плотности потока вероятности (3) на массу частицы m или на заряд частицы q можно получить вектор плотности потока массы и плотность электрического тока, переносимого частицей, находящейся в состоянии 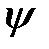. Вектор плотности потока вероятности позволяет таким способом перейти от волновых функций (решений уравнения Шрёдингера) к материальным потокам в квантовых системах и построить, например, электродинамику атомов и молекул, исследовать их магнитные свойства и т. д.

Date: 2015-05-19; view: 3521; Нарушение авторских прав