Принцип суперпозиции состояний

Пусть физическая величина f, характеризующая микрочастицу (полная энергия, угловой момент и т.д.) принимает дискретный ряд значений. Тогда, согласно постулату соответствия, эти значения можно получить, решая операторное уравнение 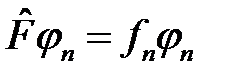, где квантовое число n классифицирует собственные значения и собственные функции оператора 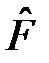. Запишем это уравнение и комплексно-сопряжённое уравнение

,

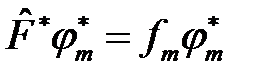где числа n и m независимо друг от друга пробегают натуральный ряд чисел: 1, 2, 3,… .

Умножим первое уравнение слева на функцию 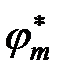, а второе – на 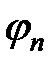и проинтегрируем по всему пространству; затем, вычитая второе уравнение из первого, получим

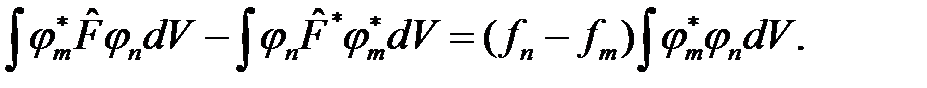
Первая часть этого уравнения равна нулю по условию эрмитовости оператора 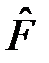. Поэтому, если 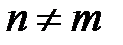, то интеграл в правой части должен быть равен нулю, т.е.

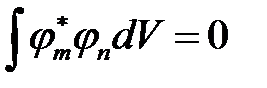. (1)

Это условие ортогональности функци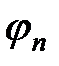й и 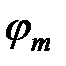. Если 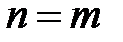, то получаем интеграл вида 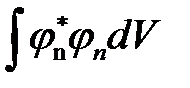, который согласно постулату состояния, равен единице, т.е.

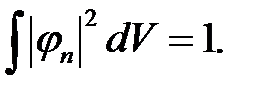(2)

Это условие нормировки волновой функции .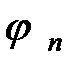

Условия ортогональности (1) и нормировки (2) можно объединить, используя символ Кроннекера :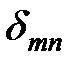

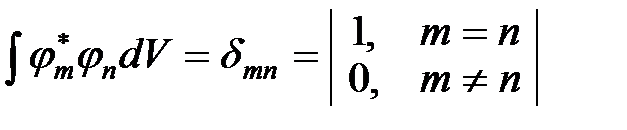. (3)

Условие (3) называют условием ортонормированности собственных функций эрмитовых операторов.

Важность этого условия состоит в том, что ортонормированные функции могут служить базисом (ортами) бесконечномерного пространства Гильберта. Тогда любую волновую функцию Ф 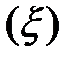можно рассматривать как вектор состояния в пространстве Гильберта, базисом которого служат собственные функции эрмитового оператора :

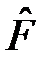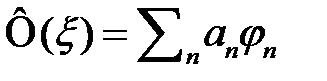. (4)

Таким образом, свойство ортонормированности (3) даёт возможность разложения любого состояния в ряд по собственным функциям любого эрмитового оператора. Разложение (4) называют разложением в обобщённый ряд Фурье, которое выражает принцип суперпозиции состояний в квантовой механике: если квантовая система может находиться в состояниях 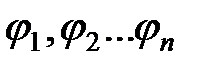, то она может находиться и в состоянии (4), представляющих их линейную комбинацию.

Функция (4) должна удовлетворять условию нормировки (см. постулат I). Подставим (4) в условие нормировки

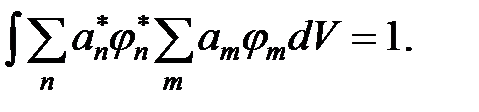
Так как суммирование производится по дискретным квантовым числам n и m, которые независимо друг от друга пробегают натуральный ряд чисел, а интегрирование производится по координатам, то

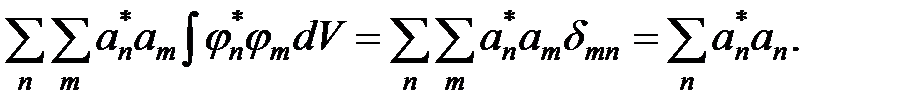
По условию нормировки эта сумма равна единице, поэтому для коэффициентов разложения получаем:

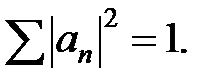(5)

Равенство (5) выражает условие полноты разложения по базису (4).

Для выяснения физического смысла коэффициентов разложения а_n рассмотрим состояние с определённым значением физической величины b, т.е. 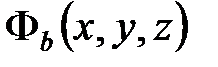. Разложим его по собственным функциям оператора 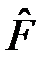, удовлетворяющих операторному уравнению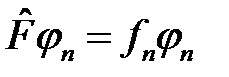

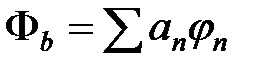. (6)

Вычислим среднее значение физической величины f в этом состоянии:

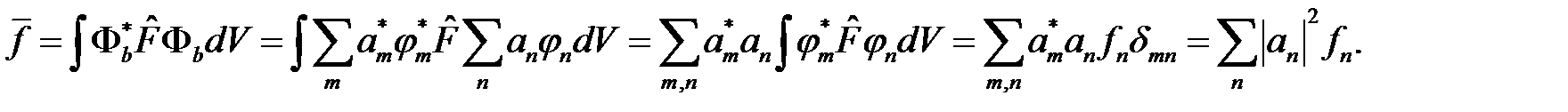Сравнивая эту формулу с известным из математической статистике выражением для среднего значения случайной величины: 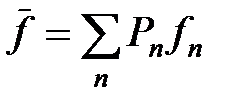, получим, что квадрат модуля 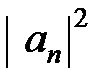есть вероятность P_n обнаружить в данном состоянии Ф_b физическую величину f, равную f_n.

Явный вид коэффициента разложения а_n можно получить, умножая выражение (6) слева на функцию 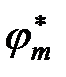, интегрируя по всему пространству и используя условие ортонормированности собственных функций эрмитовых операторов:

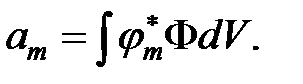(7)

Таким образом, принцип суперпозиции в квантовой механике выражается в виде разложения состояния Ф по собственным функциям эрмитовых операторов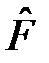

,

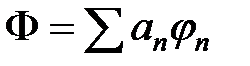где 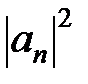есть вероятность застать систему в состоянии .

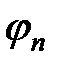1.3. Уравнение Шрёдингера, его стационарные решения

В соответствии с постулатом причинности состояние квантовой системы 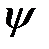является решением временнóго уравнения Шрёдингера

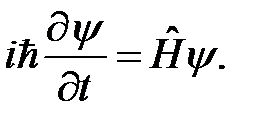(1)

Если квантовая система консервативна или находится в независящем от времени силовом поле, то оператор Гамильтона не зависит явно от времени. Такие состояния являются стационарными, т.е. с сохраняющейся полной энергией Е. Следовательно, стационарные состояния определяются как собственные функции оператора Гамильтона:

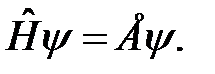(2)

Уравнение (2) называют стационарным уравнением Шрёдингера. Комбинируя (1) и (2), получим дифференциальное уравнение первого порядка:

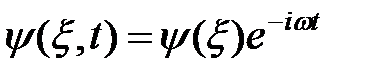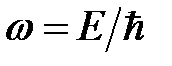Его решение есть , где , а 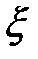– пространственная координата системы. Таким образом, стационарные состояния осциллируют во времени с частотой 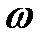, а амплитуда осцилляции 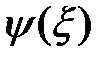есть решение стационарного уравнения Шрёдингера (2). Так как оператор Гамильтона эрмитов, то стационарные состояния ортонормированны и могут служить базисом для разложения любых состояний.

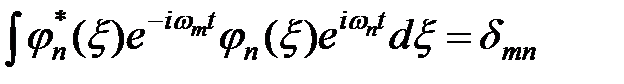. (3)

Из условия ортонормированности стационарных состояний (3), в частности, следует, что средние значения физических величин в стационарном состоянии не зависят от времени:

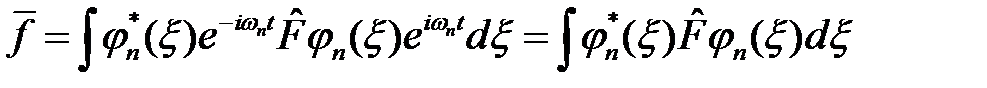. (4)

Date: 2015-05-19; view: 695; Нарушение авторских прав