
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Постулаты квантовой механики
|
|
Квантовая механика строится на дедуктивном принципе, её математический аппарат основан на постулатах. В физических курсах квантовой механики общепринятой принимается аксиоматика, содержащая три постулата: постулат состояния, постулат соответствия и постулат причинности.
I. Постулат состояния: состояние квантовой системы описывается с помощью комплексной функции 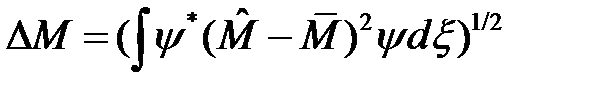 , называемой «волновой», квадрат модуля которой есть плотность вероятности
, называемой «волновой», квадрат модуля которой есть плотность вероятности
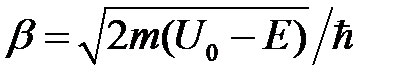 .
.
Из постулата состояния следует, что вероятность обнаружить частицу в бесконечно малом элементе объёма dV определяется выражением
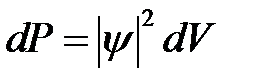 , (1)
, (1)
которое позволяет вычислять по заданной волновой функции вероятность нахождения частицы в заданном объёме  :
:
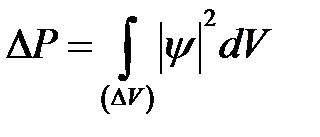 .
.
Например, в одномерном случае интеграл 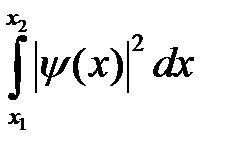 даёт вероятность нахождения частицы на отрезке от x 1 до x 2. Если интегрирование производится по бесконечному объёму
даёт вероятность нахождения частицы на отрезке от x 1 до x 2. Если интегрирование производится по бесконечному объёму 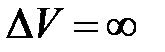 , то
, то 
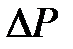 есть вероятность достоверного события, т.е.
есть вероятность достоверного события, т.е. 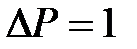 , из чего следует общее условие, которому должна удовлетворять волновая функция – условие нормировки:
, из чего следует общее условие, которому должна удовлетворять волновая функция – условие нормировки:
 . (2)
. (2)
Таким образом, в квантовой теории постулируется вероятностный способ описания состояния микрочастицы.
II. Постулат соответствия: каждой физической величине 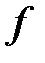 в квантовой механике ставится в соответствие эрмитов оператор
в квантовой механике ставится в соответствие эрмитов оператор 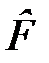 с помощью “формулы среднего”
с помощью “формулы среднего”
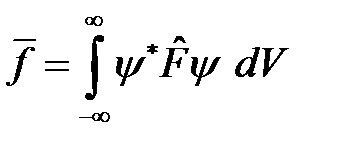 , (3)
, (3)
где 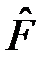 – оператор, удовлетворяющий условию эрмитовости, которое в общем случае имеет вид
– оператор, удовлетворяющий условию эрмитовости, которое в общем случае имеет вид
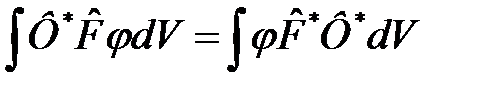 . (4)
. (4)
(Здесь и далее интегрирование производится по всему пространству).
Из условия (4) следует, что
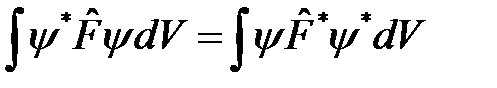 , т.е.
, т.е. 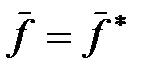 .
.
Последнее равенство выражает условие действительности физической величины f. Формула среднего (3) позволяет вычислять неопределённости физических величин в данном состоянии 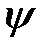 .
.
Неопределённость случайной величины f определяется выражением
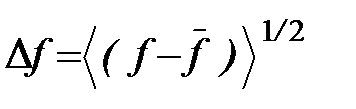
Возведём его в квадрат и воспользуемся формулой среднего
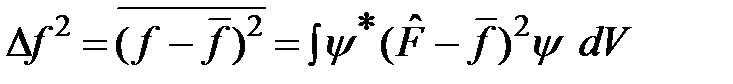 .
.
Обозначим оператор 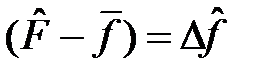 и применяя условие эрмитовости (4), получим
и применяя условие эрмитовости (4), получим
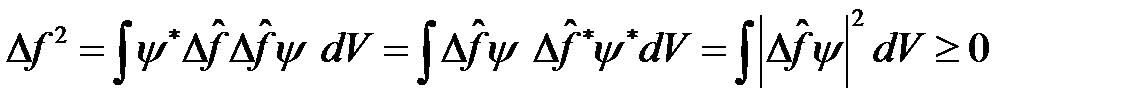 .
.
Если в состоянии 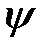 физическая величина f имеет определённое значение, то
физическая величина f имеет определённое значение, то 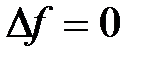 и
и 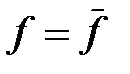 ; следовательно,
; следовательно,  и, учитывая введённое ранее обозначение
и, учитывая введённое ранее обозначение 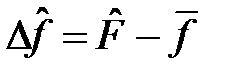 , получим
, получим
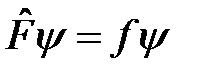 . (5)
. (5)
Уравнение (5) называется операторным, его решения 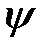 – собственные функции оператора
– собственные функции оператора 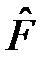 , а величины f – собственные значения оператора
, а величины f – собственные значения оператора 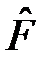 . Из
. Из
Таблица 1. Операторы основных физических величин
| Физическая величина | Эрмитов оператор | Собственные функции | Собственное значение |
координаты x, y, z
импульс 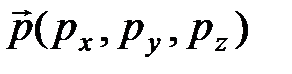 угловой момент
угловой момент 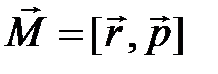 полная энергия (функция Гамильтона)
полная энергия (функция Гамильтона)
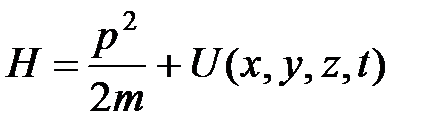
| оператор координаты – оператор умножения
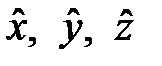 оператор импульса
оператор импульса 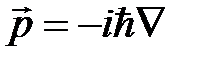
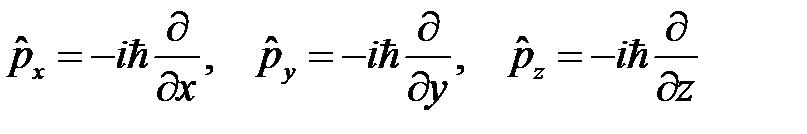 оператор углового момента
оператор углового момента 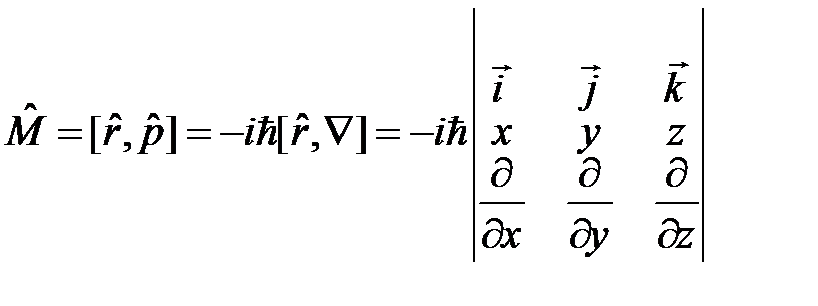 в сферической системе координат
в сферической системе координат
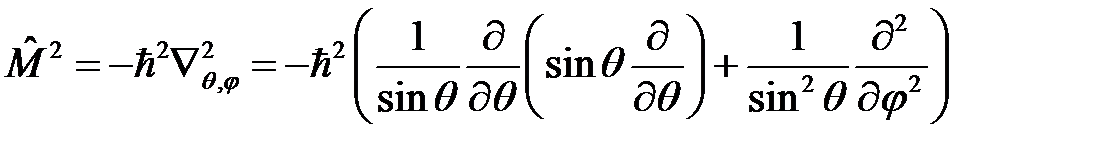 оператор Гамильтона
оператор Гамильтона
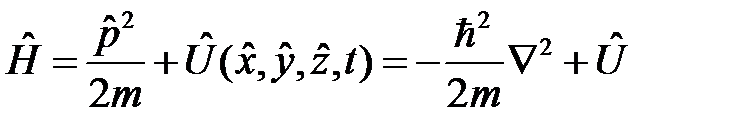
|
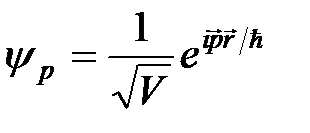 плоская волна де Бройля – состояние свободно движущейся частицы
плоская волна де Бройля – состояние свободно движущейся частицы
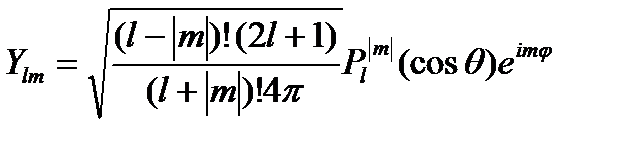 зависят от вида потенциального «рельефа»
зависят от вида потенциального «рельефа» 
| непрерывный спектр
дискретный спектр 
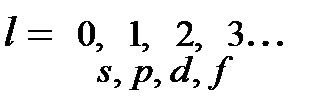
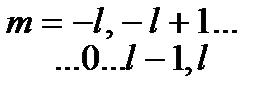 непрерывный спектр, если
непрерывный спектр, если 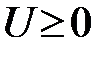 дискретный спектр, если
дискретный спектр, если 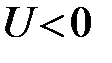
|
постулата соответствия следует, что наблюдаемые в эксперименте физические величины есть собственные значения соответствующих эрмитовых операторов. Постулируемые важнейшие операторы приведены в Таблице 1.
III. Постулат причинности
Cостояние микрочастицы 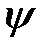 есть решение временнóго уравнения Шрёдингера
есть решение временнóго уравнения Шрёдингера
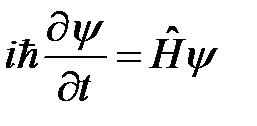 . (6)
. (6)
Уравнение Шрёдингера – дифференциальное уравнение в частных производных первого порядка по времени и второго по координатам. Оно позволяет по волновой функции в начальный момент времени 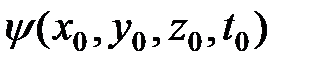 рассчитать волновую функцию частицы в произвольный момент времени t, т.е. функцию
рассчитать волновую функцию частицы в произвольный момент времени t, т.е. функцию 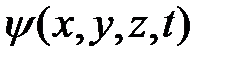 и таким образом устанавливает причинно-следственную связь между состоянием системы в настоящем и будущем.
и таким образом устанавливает причинно-следственную связь между состоянием системы в настоящем и будущем.
Date: 2015-05-19; view: 903; Нарушение авторских прав