Спектр энергии. Радиальные волновые функции. Полиномы Лаггера

Для нахождения спектра энергии электрона в кулоновском потенциале необходимо найти собственные значения оператора 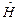, т.е. решить стационарное уравнение Шредингера (26.6). Как было выяснено в §26 решение уравнения (26.6) удовлетворяет соотношения (26.8): 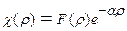, где

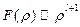(26.12)

Подставляя уравнение (26.8) в (26.6) получим уравнение для функции :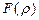

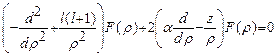. (27.1)

Будем искать решение уравнения (27.1) в виде степенного ряда:

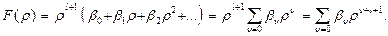(27.2)

Подставляя (27.2) в (27.1) путём не сложных вычислений получим соотношение:

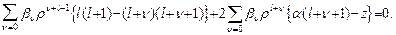
или, заменяя в первом слагаемом 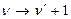и перенося второе слагаемое в правую часть, получим:

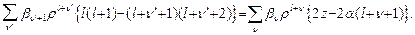(27.3)

Считая 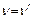приравняем коэффициенты при одинаковых степенях 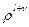. Откуда получим рекурентное соотношение для коэффициентов :

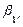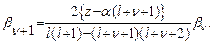(27.4)

Исследуем соотношение (27.4) при 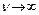. Получим, что 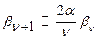. Откуда 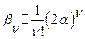и 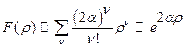. Тогда, согласно соотношению (26.8) 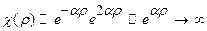. Следовательно, ряд (27.2) должен быть конечен, т.е.

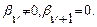(27.5)

Тогда из рекурентного соотношения (27.4) получим соотношение:

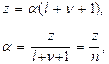(27.6)

,где

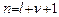, (27.7)

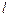-орбитальное квантовое число, 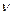- радиальное квантовое число.

Из соотношения (26.7) с учётом (27.6) и (27.7) имеем:

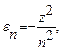
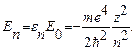(27.8)

Уравнение (27.8) определяет спектр значений энергии электрона в атоме водорода (при 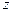=1). Таким образом, уравнение Шредингера (26.6) имеет непрерывные, однозначные и конечные решения лишь при дискретных значениях энергии, т.е. энергия электрона в атоме водорода квантуется.

Отметим, что знак «минус» в (27.8) означает лишь, что в качестве нуля энергии была выбрана энергия электрона, расположенного вдалеке от протона.

Для атома водорода (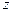 =1) радиальная волновая функция имеет вид:

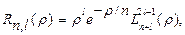(27.9)

где 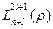- полиномы Лаггера, которые имеют вид:

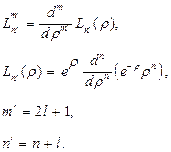(27.10)

Простейшие радиальные волновые функции 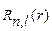имеют следующий вид.

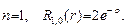(27.11)

Таким образом, если атом водорода находится в своём основном состоянии, то амплитуда того, что электрон будет обнаружен в каком-то месте, экспоненциально падает с расстоянием от протона. Вероятнее всего встретить его вплотную близ протона на расстоянии одного боровского радиуса .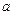

При более высоком уровне 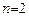,получаем:

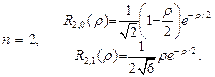(27.12)

Date: 2015-05-18; view: 585; Нарушение авторских прав