Необходимые и достаточные признаки симметрии

Рассмотрим математическую формулировку преобразований симметрии.

Введем некоторый оператор 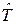, который действует на любое состояние системы 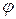по правилу:

,

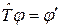где 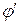- новое состояние системы.

И потребуем, чтобы обратное преобразование 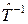переводило систему обратно в исходное состояние, т.е.

.

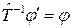Таким образом, из этих соотношений следует, что 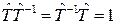, т.е. произведение 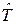и 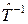есть тождественное преобразование.

Все операции в квантовой механике инвариантны относительно этого преобразования. Рассмотрим оператор 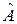: 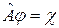и подействуем на это выражение оператором :

.

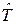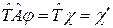Если на систему еще подействовать тождественным оператором 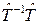, то мы получаем такое выражение:

.

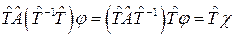Обозначим оператор 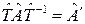и тогда получим выражение:

.

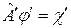Таким образом, любое соотношение между физическими величинами после преобразования 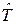не меняет вид:

.

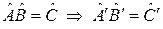Найдем класс преобразований, которые оставляют без изменения измерения. Для этого выясним вид оператора, при котором амплитуда вероятности оставалась бы без изменений. Потребуем, чтобы 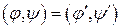. Подробнее рассмотрим :

.

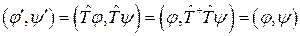Таким образом, из рассмотренного соотношения вытекает, что данное преобразование оставляет амплитуду вероятности неизменной, если 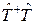равен единичному оператору, т.е.

.

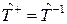А это есть унитарное преобразование.

При унитарном преобразовании эрмитовский оператор переходит в эрмитовский. Покажем это. Пусть 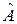- эрмитовский оператор. Докажем, что после унитарного преобразования 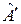тоже будет эрмитовским оператором. Здесь 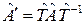. То есть нужно доказать тот факт, что если 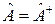, то после преобразования должно получиться .

.

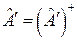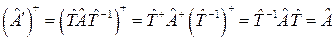Унитарное преобразование 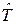есть преобразование симметрии данной физической системы, если после преобразования не меняются уравнения физической системы.

Будем исходить из уравнения Шредингера:

.

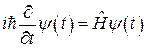Определим класс преобразований 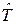: 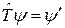, не меняющих это уравнение, то есть нужно посмотреть, при каких условиях преобразование 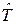переводит уравнение Шредингера для вектора 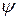в уравнение такого же вида только для вектора .

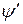Для этого подействуем на уравнение Шредингера оператором :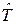

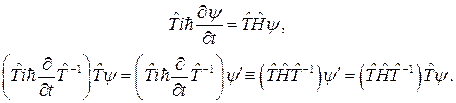
Таким образом, у нас есть два условия (необходимое и достаточное), при выполнении которых преобразование 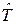есть преобразование симметрии:

1)

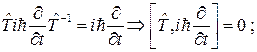
2)

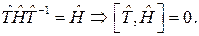
Date: 2015-05-18; view: 420; Нарушение авторских прав