Спин электрона и релятивистская теория. Уравнение Дирака

Теории Шредингера и Паули носят нерелятивистский характер. Дирак в 1928 году обобщил уравнение Паули на теорию относительности и получил релятивистски инвариантное уравнение, описывающее движение электрона 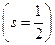в магнитном поле.

Рассмотрим сначала уравнение Дирака для свободного электрона (в отсутствие внешних полей). В этом случае классическое выражение функции Гамильтона в теории относительности имеет вид:

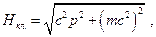(25.1)

где 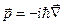. Согласно правилам квантования

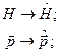
и с учетом спина электрона

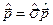
запишем

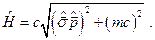(25.2)

Для нахождения явного вида оператора Гамильтона 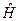необходимо извлечь корень 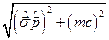. Для этого введем матрицы 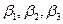, аналогичные матрицам Паули, такие, что

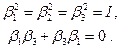(25.3)

Нетрудно показать, используя свойства (25.3), что

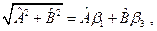(25.4)

при условии, что 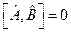. Откуда с учетом (25.4) оператор Гамильтона (25.2) примет вид:

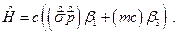(25.5)

Введя обозначени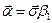е , где 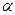- так называемые матрицы Дирака, и выбирая на роль 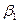и 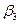матрицы:

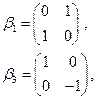
запишем уравнение Дирака для свободного электрона

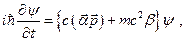(25.6)

где 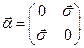, , 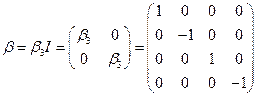а .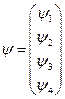

Таким образом, уравнение Дирака – это фактически система четырех уравнений для 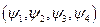от .

Огромным успехом теории электрона Дирака стало теоретическое предсказание существования позитрона, который вскоре после этого и был обнаружен.

Обобщим полученное уравнение (25.6) на случай электромагнитного поля. Очевидно, что для этого достаточно произвести замену 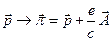и прибавить потенциальную энергию :

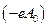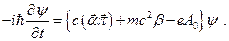(25.7)

Уравнение Дирака – это релятивистски инвариантное уравнение для частицы со спином 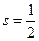, т.е. для ферми-частицы.

Date: 2015-05-18; view: 674; Нарушение авторских прав