Свойства сферических гармоник и их явные выражения

Остановимся на свойствах шаровых функций, следующих из общей теории момента.

1)Сферические гармоники 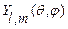являются общими собственными функциями операторов 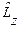и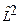

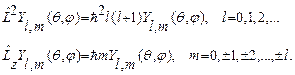
2)Сферические гармоники удовлетворяют следующему условию ортонормировки:

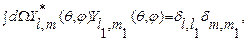(28.6)

где 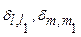- символы Кронекера, которые определяются следующим соотношением

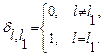
а 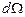- элемент объёма.

Иначе условие (28.6) можно записать в виде:

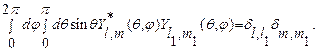
Условие нормировки с учётом (28.5) примет вид:

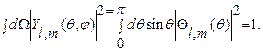
3)Из общей теории момента следует:

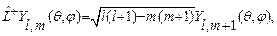(28.7)

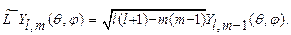(27.8)

В частности, из уравнения (28.7) следует:

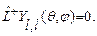(28.9)

Перечисленных свойств достаточно для выполнения любых расчётов, связанных с шаровыми функциями.

Для нахождения угловой зависимости сферических гармоник следует воспользоваться явным выражением оператора 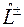в сферической системе координат. Подставляя (28.2) и (28.5) в (28.9) получим дифференциальное уравнение

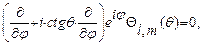(28.10)

решение которого имеет вид:

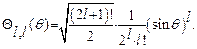(28.11)

Ниже в таблице приведён вид некоторых сферических гармоник.

Таблица. Сферические гармоники.

l	m	Угловая зависимость амплитуд	Состояние	Чёт-ность
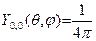
			S	+
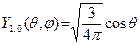
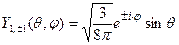
	±1		P	-
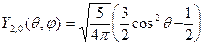
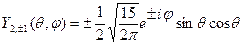
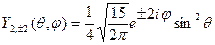
	±1     ±2		D	+
l	m		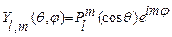	(-1)l

Рассмотрим распределение амплитуд наблюдения электрона в том или ином месте атома водорода на примере электрона в р-состоянии (m=0): 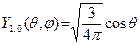. Это означает, что амплитуда положительна в верхней части (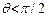), отрицательна в нижней части (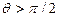) и равна нулю при 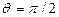. Возводя её в квадрат получим зависимость вероятности от 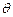(см. рис).

28.3 Закон сохранения чётности.

Сферические функции 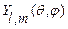обладают определённой чётностью при преобразовании :

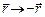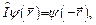
причём оператор этого преобразования 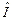, называемый чётностью, удовлетворяет следующим соотношениям:

Собственные значения оператора 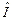принимают лишь два значения 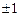, в зависимости от .

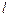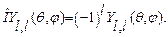
1) Если 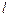- чётное, то 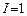и волновая функция описывает чётное состояние (см. таблицу).

2) Если 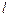- нечётное, то 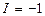и волновая функция соответствует нечётному состоянию.

Date: 2015-05-18; view: 1170; Нарушение авторских прав