Сложение квантовых моментов

Как правило, при анализе физических явлений приходится иметь дело со сложной системой, состоящей из нескольких подсистем. При этом возникает вопрос о правилах сложения квантовых моментов, которые существенно отличаются от сложения векторных классических величин. Эта проблема существует даже для отдельной частицы, имеющей собственный момент – спин. Полный момент в этом случае будет состоять из 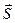и : .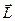

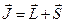Пусть система состоит из двух подсистем с квантовыми моментам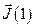и и 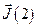соответственно. Тогда в силу аддитивности момента квантовый момент системы равен:

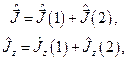
где 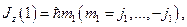аналогично 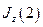. Также будем считать, что заданы величины:

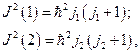
и пусть они не меняются в процессе взаимодействия. Тогда 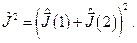Но с другой стороны, 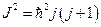. Возникает вопрос: какие значения может принимать 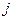при заданных квантовых числах 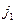и 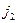? Прежде чем решать поставленную задачу, выберем систему базисных векторов.

Для подсистемы (1) можно одновременно задать 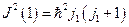и 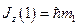. Состояние подсистемы можно описать с помощью волновой функции 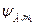. Аналогично, для подсистемы (2): .

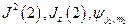Поскольку операторы моментов, относящихся к разным подсистемам, коммутируют друг с другом, то следующие величины одновременно измеримы и образуют полный набор: 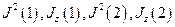. Соответствующие им квантовые числа: 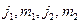. Собственный вектор, характеризующий состояние всей системы, есть: 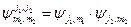. Число таких независимых состояний: 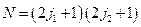. Таким образом, система базисных векторов 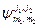является полной, и любой вектор состояния может быть разложен следующим образом:

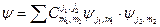. (23.1)

Существует и другая возможность выбора системы базисных векторов. Можно задать полный момент всей системы 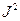и его проекцию 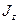, так как

.

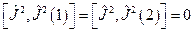Таким образом, величины 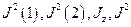образуют полный набор величин с соответствующими квантовыми числами 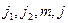. Система базисных векторов 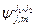состоит из 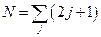векторов. Любое состояние можно разложить по базисным векторам .

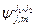Итак, существуют два набора базисных векторов, т.е. два способа задания состояния квантовой системы. Отметим особенности этих двух базисов. Из определения оператора полного момента 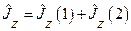следует, что есл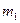и и 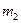заданы, то задана и проекция полного момента. Т.к. 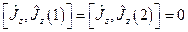, то

;

.

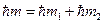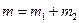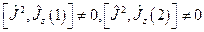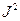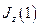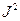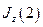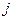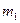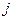Однако, , т.е. нельзя одновременно задать и ; и , а значит и , и 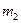. Эту наиболее важную особенность можно наглядно изобразить на векторной модели сложения моментов. Квантовые числа 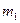и 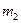нельзя фиксировать одновременно с .

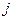Любой из базисных векторов 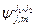можно разложить по полному набору :

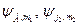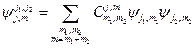. (23.2)

Коэффициенты разложения 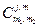называют коэффициентами Клебша-Гордона. Квадрат модуля 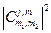показывает вероятность измерения проекции 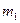, 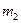при заданных числах .

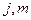Очевидно, что можно записать и обратное разложение:

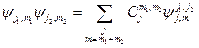. (23.3)

Коэффициенты 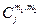называются обратными коэффициентами Клебша-Гордона. Они взаимосвязаны с коэффициентами .

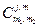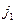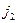Пусть и – фиксированные, т.е. 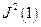и имеют определенные значения, которые не меняются в процессе взаимодействия.

Каковы же возможные значения 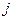при фиксированных 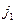и 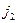? Для ответа на этот вопрос рассмотрим следующую теорему.

Теорема: При заданных значениях квадратов моментов двух частей системы 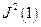, , определяемых квантовыми числам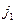и и 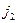, значение квантового числа 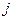, определяющего квадрат полного момента 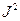, принимает следующий ряд значений:

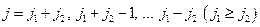. (23.4)

Доказательство: Для доказательства воспользуемся следующими свойствами:

1) ;

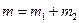2) ;

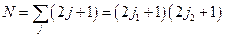3) ;

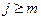4) .

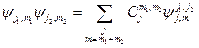Будем считать для определенности, что 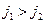. Пусть 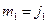(поворот системы координат). Тогда 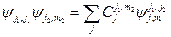, здесь 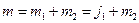. Мы предположили, что 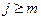, следовательно, мы можем положить:

.

Для нахождения возможных значений 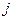будем перебирать различные значения 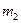: 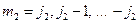. Тогда 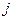будет принимать следующий ряд значений:

.

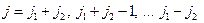Докажем, что других значений 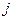нет. Число базисных векторов :

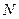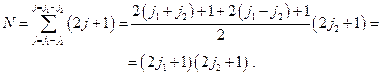
Т.е. других значений квантовое число 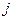иметь не может. Теорема доказана.

В качестве простейшего примера на сложение квантовых моментов мы рассмотрим сложение двух спинов.

Пусть имеется квантовая система, состоящая из двух электронов. Квантовые числа, соответствующие спинам электронов: 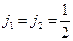. Обозначим спиновое состояние частицы с проекцией 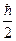на ось 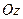- 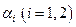, а с проекцией 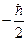– 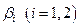. Таким образом, получим всего четыре независимых спиновых состояния с определенной проекцией 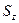каждого спина: 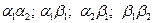. Любое состояние квантовой системы из двух электронов может быть представлено как суперпозиция четырех базисных векторов.

Теперь рассмотрим состояни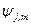е , где 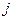- суммарный спиновый момент, 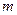- проекция полного момента. По правилу сложения имеем:

.

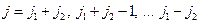Отсюда следует, что .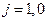

При 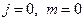возможно только одно состояние системы 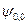. Такое состояние называется синглетным.

При 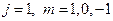возможны три состояния: 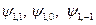. Такое состояние системы называется триплетным. Таким образом, любое состояние системы можно выразить через четыре этих вектора.

Теперь свяжем между собой два базисных набора, т.е. найдем коэффициенты Клебша-Гордона. Т.к. 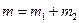и 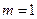, то можно сделать вывод, что 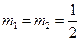, т.е. 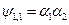. Аналогично показывается, что .

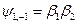Построим теперь :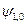

.

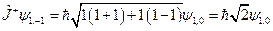С другой стороны, 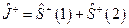. Подействуем оператором 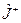на вектор :

,

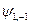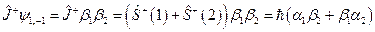где .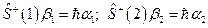

Приравниваем эти выражения и получаем:

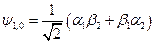
Остается построить еще синглетное состояние :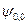

.

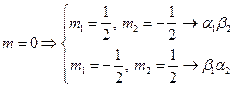Таким образом, 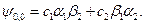Векторы 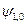и 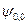нормированные, поэтому .

,

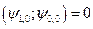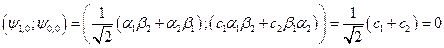т.к. векторы 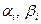тоже нормированные вектора. Следовательно, 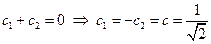. Окончательно получаем, что

.

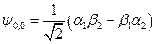На основе полученных формул можно сделать вывод: триплетное состояние симметрично относительно перестановки спинов, а синглетное состояние антисимметрично.

Date: 2015-05-18; view: 766; Нарушение авторских прав