Движение частиц в сферически симметричном потенциале. Интегралы движения. Полный набор физических величин и их общие собственные функции

Рассмотрим квантовые системы, обладающие сферической симметрией. К данному классу относятся наиболее часто встречающиеся задачи квантовой физики:

1) задачи по определению уровней энергии связанных состояний атомов, ионов и других атомоподобных систем;

2) задачи о рассеянии квантовых частиц.

Квантовая система в нерелятивистском приближении будет обладать сферической симметрией, если может быть выбрана система координат, в которой гамильтониан 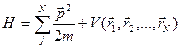не меняется при вращении.

Для наглядности рассмотрим частный случай – отдельную частицу в сферически симметричном потенциале без учёта спина s. Гамильтониан частицы имеет вид:

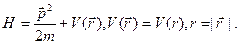(25.1)

В случае сферически-симметричного поля, когда потенциал поля зависит только от (а не от и), вращение относительно любой оси оставляет неизменным гамильтониан 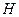. Отсюда следует и сохранение момента количества движения и всех его проекций. Таким образом, 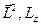являются интегралами движения.

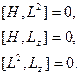(25.2)

Из соотношений (25.2) следует, что величины - одновременно измеримы, т.е. составляют полный набор величин, задание которого определяет состояние квантовой системы. Иначе говоря, состояние квантовой системы однозначно задаётся квантовыми числами .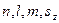

Согласно рассмотренной выше теореме, если операторы коммутируют, то они имеют общую полную систему собственных функций. Общие собственные функции операторов 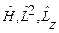одновременно удовлетворяют уравнениям:

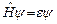,. (25.3)

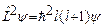, (25.4)

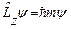. (25.5)

Для нахождения спектра значений энергии 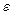, определяемого уравнением (25.3), следует отыскать функции, которые являются одновременно собственными функциями операторов 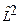и 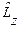. Для определения спектра значений энергии квантовой частицы в сферическом потенциале 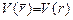будем искать решение (25.3) в виде:

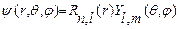, (25.6)

Где 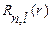-радиальная, а 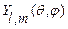- сферическая (шаровая) волновые функции. Так как 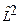и 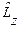зависят только от угловых переменных 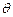и , то функции 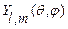удовлетворяют уравнениям:

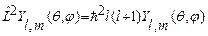, (25.7)

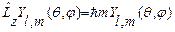. (25.8)

Подставляя (25.1) и (25.6) в (25.3) получим следующее радиальное уравнение Шредингера для квантовой частицы в сферически-симметричном потенциале:

.

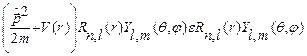Выразим гамильтониан системы 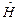в сферической системе координат. Поскольку 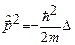, то для этого достаточно выразить оператор Лапласа в сферической системе координат. Мы же воспользуемся для этого принципом соответствия. Для этого запишем функцию Гамильтона в сферической системе координат, а затем перейдём к операторному равенству.

.

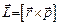Используя формулу получим:

,

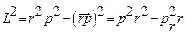где

.

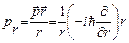Откуда .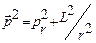

Таким образом, в сферической системе координат выглядит следующим образом:

.

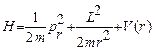Откуда по принципу соответствия оператор Гамильтона имеет вид:

,

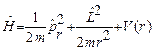Или

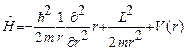(25.9)

Используя явный вид оператора 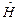в сферической системе координат (25.9) и подставляя решение 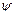в виде (25.6) получим стационарное уравнение Шредингера:

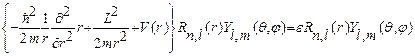. (25.10)

Date: 2015-05-18; view: 1069; Нарушение авторских прав