Уравнение Паули. Собственный магнитный момент электрона

Основным уравнением нерелятивистской квантовой механики является уравнение Шредингера, описывающее движение нерелятивистской частицы без учета спина:

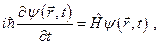
где 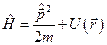- оператор Гамильтона. Теория Шредингера исходила из предположения, что электрон обладает лишь степенями свободы, которые соответствуют движению материальной точки в пространстве координат .

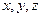Введение же новой степени свободы, связанной со спином, дает новые возможности для перехода от величин классической механики к квантовым операторам и позволяет построить оператор

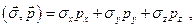(24.1)

где 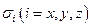- матрицы Паули, а 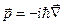- импульс частицы. Оператор (24.1) может быть использован при построении оператора энергии.

Произвольное состояние электрона при учете спина записывается в виде двухрядной матрицы

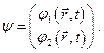
Вследствие этого и гамильтониан 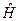тоже должен быть двухрядной матрицей и, согласно свойствам матриц Паули, может быть представлен через матрицы Паули 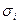и единичную матрицу .

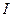Гамильтониан не должен зависеть от направлений, т.е. пространственные переменные должны входить в гамильтониан равноправным образом и в то же время он должен включать в себя матрицы Паули 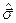. Таким образом, из соображений размерности можно положить, что гамильтониан свободной частицы с учетом спина имеет вид:

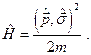(24.2)

Используя свойства матриц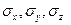

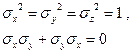
и коммутативность операторов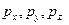

,

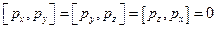вычислим квадрат скалярного произведения :

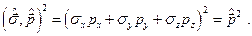
Откуда

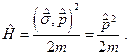
Как и следовало ожидать в отсутствие внешних полей наличие спина никоим образом не проявляется, и введение оператора, определяемого формулой (24.1), здесь ничего не вносит.

Иначе обстоит дело при наличии магнитного поля, когда классическая функция Гамильтона электрона в электромагнитном поле с векторным потенциалом 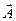и скалярным потенциалом 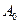имеет вид:

Согласно правилам квантования

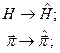
и учитывая наличие спина у электрона

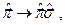
оператор Гамильтона примет вид:

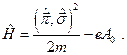(24.3)

Рассмотрим квадрат скалярного произведения операторов и :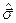

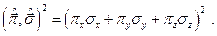
Используя свойства матриц Паули, получим

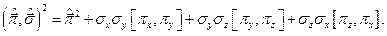
Учитывая выражения, справедливые для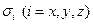

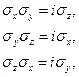
квадрат скалярного произведения примет вид:

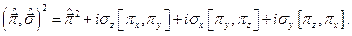(24.4)

В данном случае операторы 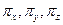не коммутативны, а удовлетворяют перестановочным соотношениям:

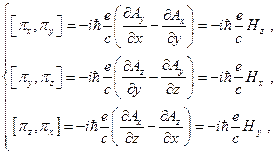(24.5)

где 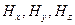- составляющие магнитного поля.

Оператор Гамильтона (24.3) с учетом (24.4), (24.5) примет вид:

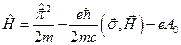(24.6)

или

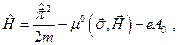(24.7)

где постоянная есть магнитный момент электрона. Таким образом, наличие спина у электрона влечет за собой наличие собственного магнитного момента электрона.

Определив выражение оператора Гамильтона (24.7), запишем волновое уравнение, называемое уравнением Паули, которое описывает состояние электрона в магнитном поле без поправки на теорию относительности:

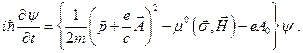(24.8)

Date: 2015-05-18; view: 530; Нарушение авторских прав