Движение электрона в кулоновском потенциале. Стационарное уравнение Шредингера для радиальной составляющей волновой функции. Асимптотика уравнения на малых и больших расстояниях

Рассмотрим движение электрона в кулоновском потенциале (например, электрон в атоме водорода или водородоподобных атомах). Для полного описания атома водорода следовало бы учесть: во-первых, движение обеих частиц – как протона, так и электрона; а во вторых, наличие спина у электрона. Мы используем два приближения:

1) будем считать протон очень тяжёлым (настолько, что он как бы закреплён в центре атома);

2) будем рассматривать электрон как частицу без спина.

Небольшие магнитные эффекты появляются из-за того, что протон с точки зрения электрона есть циркулирующий по кругу заряд, который создаёт магнитное поле. Энергия электрона в этом поле будет различна, в зависимости от направление спина. В результате этого энергия атома будет немного сдвинута относительно ниже вычисленной величины. Мы пренебрежём этим слабым сдвигом энергии и вообразим, что электрон подобен волчку, движущемуся в пространстве по кругу и сохраняющему всё время одинаковое направление спина.

Поскольку речь идёт о свободном атоме в пространстве, полный момент количества движения будет сохраняться. В нашем приближении будет считаться, что момент количества движения, вызываемый спином электрона считается неизменным, так что оставшийся момент количества движения атома («орбитальный» момент количества движения) также не будет изменяться. В очень хорошем приближении можно считать, что электрон движется в атоме водорода как частица без спина – его орбитальный момент количества движения постоянен.

Для решения задачи воспользуемся уже полученными уравнениями, описывающими движение частиц в сферически-симметричном потенциале.

Запишем стационарное уравнение Шредингера для радиальной составляющей волновой функции. Для этого перепишем уравнение (25.10) в виде:

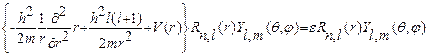
Откуда сократив на 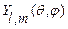и домножив левую и правую на 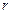получим:

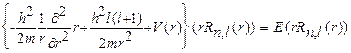(26.1)

Будем искать решение этого уравнения в виде

(26.2)

После введения безразмерной переменной

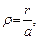(26.3)

где 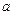- радиус первой боровской орбиты, получим стационарное уравнение Шредингера для частицы в кулоновском потенциале :

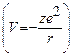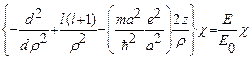, (26.4)

где

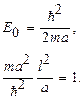(26.5)

Из уравнения (26.4) получим 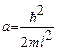и подставив в (26.5) имеем:

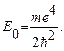
Перепишем уравнение (26.4) в следующем виде

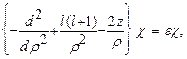(26.6)

где

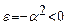, (26.7)

т.к. рассматриваем связанные состояния.

Рассмотрим асимптотику уравнения (26.6) на больших и малых расстояниях, т.е при: а) ;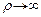

б) .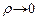

а) .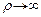

При этом условии уравнение (26.6) с учётом (26.7) примет вид:

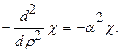
Данному уравнению удовлетворяет функция 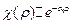, которая стремится к нулю, при. 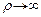Таким образом, 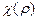можно записать в следующем виде

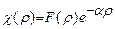. (26.8)

Задача теперь просто свелась к отысканию подходящей функции .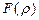

б) .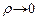

При данном условии уравнение (26.6) примет вид:

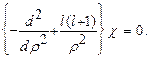(26.9)

Данному уравнению удовлетворяет функция

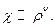(26.10)

Из уравнений (26.9) и (26.10) получим уравнение

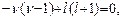
которое имеет два корня:

Рассмотрим последовательно оба варианта.

1)

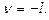
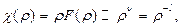
откуда 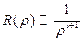, т.е. 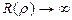, при 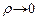. Вследствие чего (из соображений ограниченности волновой функции) данное решение отбрасывается.

3) .

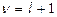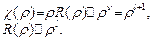
Таким образом,

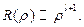(26.11)

Из равенств (26.8) и (26.11) получим следующее соотношение для :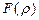

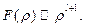(26.12)

Date: 2015-05-18; view: 582; Нарушение авторских прав