Шаровые функции

Общая теория момента одинаково применима как для собственного момента (спина), так и для орбитального и, в силу аддитивности момента, полного момента всей системы.

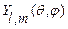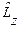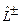Сферические гармоники (шаровые функции) есть собственные функции в сферической системе координат . Найдём их угловую зависимость, используя общую теорию момента. Для этого воспользуемся явным выражением и в сферической системе координат:

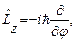(28.1)

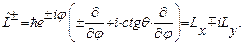(28.2)

Известно, что операторы проекции момента количества движения 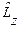и квадрата орбитального момента 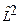одновременно измеримы, т.е. 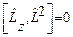. Следовательно, они обладают общей системой собственных векторов, т.е.

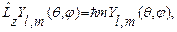(28.3)

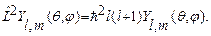(28.4)

Из уравнений (28.1) и (28.3) получим уравнение:

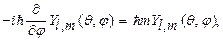
решение которого

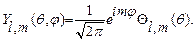(28.5)

В соответствие с условиями, накладываемыми на волновую функцию, функция 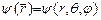должна быть однозначной. Это возможно в том случае, если она периодична по с периодом 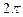, т.е. 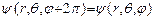. Учитывая уравнение (28.5) имеем: . Этому условию удовлетворяют лишь целые значения 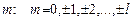. А т.к. 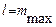, то 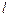тоже принимает лишь целые значения: .

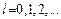Date: 2015-05-18; view: 461; Нарушение авторских прав