Спин электрона. Матрицы Паули и их свойства

Операторы спина обозначаются 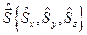. Все выражения, полученные в § 19, 20 для общего момента 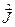справедливы как для орбитального 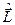, так и для спинового момента 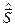. Поэтому, согласно общей теории момента,

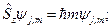(22.1)

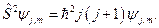(22.2)

Спин может иметь как целые, так и полуцелые значения. В соответствие с этим выделяют два класса частиц: с целым спином – бозе-частицы и с полуцелым спином – ферми-частицы.

Рассмотрим элементарный случай, когда :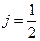

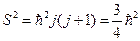. (22.3)

И проекцию спина на произвольно выбранное направление, например на ось OZ:

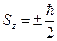. (22.4)

Т.к. операторы спина коммутируют с операторами координаты и импульса, то полный набор физических величин с учётом спина может быть представлен двумя комбинациями:

1)

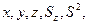
2)

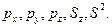
Представим спиновые операторы и состояния системы в матричном виде (в 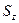–представлении). Для этого сначала выберем базисные вектора. Т.к. 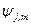определяет состояние частицы с учётом спина, то введём следующие обозначения:

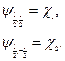(22.5)

где 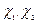- ортонормированные вектора выбранного базиса. Любое состояние 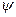можно записать с помощью этих базисных векторов:

,

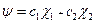где вектор 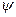нормированный, т.е. 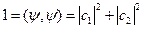. В состоянии 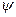при измерении проекции спина на ось OZ мы получим значение 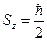с вероятностью 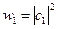и 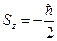с вероятностью 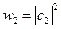. Таким образом, вектор 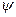можно записать как .

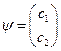Найдём вид матрицы 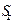в 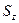-представлении.

,

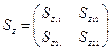где элементы матрицы вычисляются следующим образом:

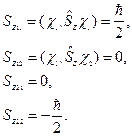
Откуда

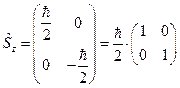. (22.6)

Для нахождения вида операторов 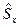и 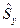определим вид операторов 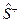и . Согласно уравнению (20.22)

,

,

.

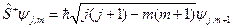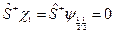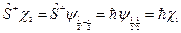Тогда

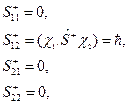
и матрица 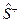примет вид

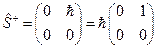. (22.7)

Матрица получается из матрицы 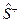путём перестановки строк и столбцов матрицы (транспонирования матрицы ):

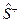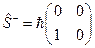. (22.8)

Операторы 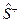и выражаются через операторы 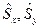следующим образом:

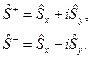
Откуда получаем вид операторов 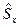и :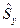

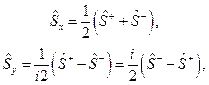
или

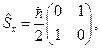(22.9)

(22.10)

Таким образом, для случая 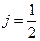спиновые матрицы являются двухрядными. Принято записывать их в следующем виде:

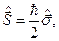(22.11)

где 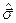- матрицы Паули в 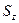-представлении:

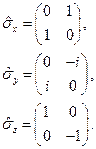(22.12)

Матрицы Паули обладают следующими свойствами.

Свойство 1. Любая двухрядная матрица может быть представлена через матрицы Паули и единичную матрицу.

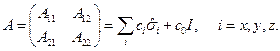(22.13)

Свойство 2. Собственные значения любой матрицы Паули есть .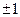

Найдём матричное представление собственных векторов матрицы Паули (например ) .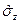

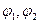С одной стороны,

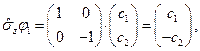
с другой

.

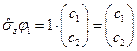Откуда

,

.

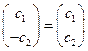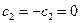Таким образом, 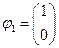. Аналогичным образом находим .

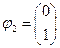Аналогично определяются собственные вектора операторов .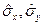

Свойство 3.

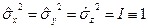. (22.14)

Доказательство. Доказательство проведём для оператора .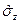

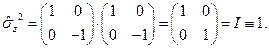
Свойство 4.

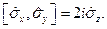(22.15)

Свойство5.

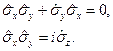(22.16)

Доказательство. Следует из свойства 4.

С учётом спина волновая функция должна зависеть не только от пространственных переменных, но и от спиновых: .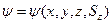

Рассмотрим состояние электрона с учётом спина:

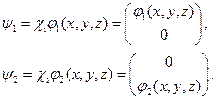
Согласно принципу суперпозиции состояний, если система может находиться в состояниях 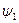и 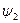, то она может находиться и в состоянии

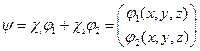. (22.17)

где 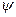- нормированный вектор. Матрица (22.17) называется спинором.

Date: 2015-05-18; view: 961; Нарушение авторских прав