Орбитальный и спиновый моменты. Спин как внутренняя степень свободы

Состояние с заданным значением 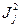вырождено с кратностью 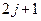по значениям проекции момента 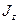, т.е. при заданном значении 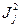проекция момента может принимать (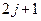) отличающихся на единицу значений: 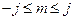. Поэтому 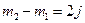должно быть целым, откуда следует заключение о значениях квантового числа 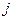: оно может быть как целым, так и полуцелым.

Это объясняется тем, что квантовый момент может быть связан как с пространственным движением частицы (орбитальный момент), так и с собственным внутренним моментом квантовой частицы, называемым спином.

Легко показать, что проекция орбитального момента частицы может быть только целой. Орбитальный момент импульса частицы 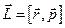достаточно хорошо изучен в классической механике. В квантовой механике проекция орбитального момента импульса в сферической системе координат имеет вид:

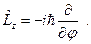(21.1)

Используя выражение (21.1) определим спектр значений проекции орбитального момента импульса 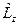. Для этого необходимо решить задачу на собственные значения и собственные функции оператора :

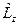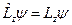
или

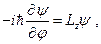(21.2)

где 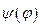- непрерывная, однозначная, ограниченная функция.

Будем искать решение в виде

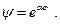(21.3)

Подставляя (21.3) в выражение (21.2), определим значение постоянной :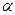

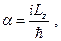
откуда волновая функция 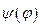примет вид

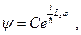
где постоянную 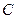определим из условия нормировки :

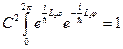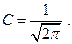
Таким образом, волновая функция имеет вид:

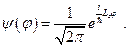(21.4)

Функция (21.4) должна удовлетворять условию

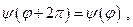(21.5)

согласно условию однозначности функции. Подставляя (21.4) в (21.5), получаем

или

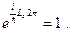
Данное выражение имеет место при выполнении условия

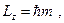(21.6)

где 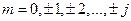- магнитное квантовое число.

Таким образом, целые значения 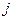соответствуют орбитальному моменту, а полуцелые связаны с собственным механическим моментом частицы – спином.

Затруднительно представить механическую модель спина. Это внутренняя степень свободы квантовой частицы, которая не имеет классического аналога.

Date: 2015-05-18; view: 425; Нарушение авторских прав