Собственные значения и собственные векторы проекции и квадрата момента

Основная задача квантовой теории момента заключается в определении общих собственных векторов и собственных значений проекции и квадрата момента. Из одновременной измеримост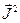и и 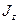следует, что соответствующие операторы этих величин имеют общую систему собственных функций :

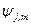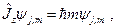(20.1)

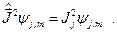(20.2)

Рассмотрим некоторые свойства оператора момента количества движения.

Свойство 1: При фиксированном значении квадрата момента количества движения 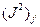проекция момента 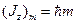принимает значения из интервала:

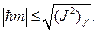(20.3)

Доказательство: Для доказательства этого свойства воспользуемся определением:

.

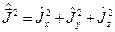Подействуем оператором квадрата момента 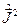на вектор состояния :

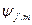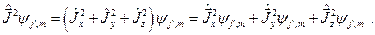
Умножая последнее выражение на 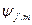и интегрируя по всей области изменения переменных получим:

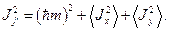
Тогда, учитывая, что средние значения не отрицательны, приходим к выводу:

т.е. максимальная проекция момента не превосходит длины вектора момента количества движения:

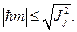
что и требовалось доказать.

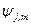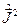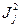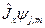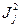Свойство 2: Если - собственный вектор оператора квадрата момента с собственным значением , то и также собственные вектора оператора квадрата момента с тем же собственным значением ,т.е.

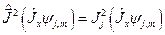, (20.4)

(20.5)

Доказательство: Подействуем оператором 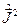на вектор состояния 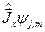и воспользуемся свойством (19.4):

,

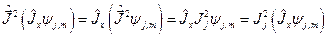Аналогично проводится доказательство для вектора .

Таким образом, из коммутируемости операторов проекци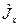й и 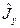с оператором квадрата момента импульса 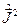следует, что их действие на вектор состояния 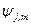не меняет .

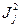Вместо операторов 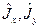удобно перейти к их комплексным комбинациям:

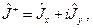(20.6)

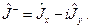(20.7)

Выразим имеющиеся соотношения через введенные комплексные операторы. Для этого найдем коммутатор :

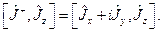
Для дальнейших вычислений воспользуемся свойством коммутатора:

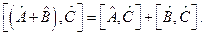
Тогда:

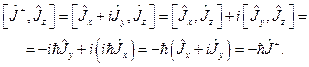(20.8)

Можно показать, что

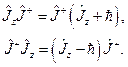(20.9)

Аналогично проводятся вычисления для :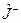

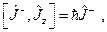(20.10)

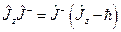. (20.11)

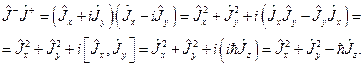(20.12)

Откуда, учитывая определение квадрата момента 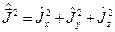следует, что

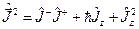(20.13)

или

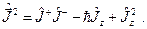(20.14)

Для решения задачи о нахождении спектра собственных значений операторов 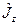и 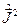рассмотрим несколько вспомогательных теорем.

Лемма 1: Если 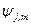- собственный вектор оператора 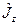с собственным значением 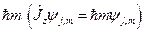, то вектор 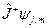тоже собственный вектор оператора 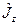с собственным значением , т.е.

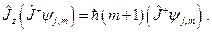
Доказательство: Подействуем оператором на вектор 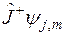. С учетом равенств (20.9) и (20.1) получаем:

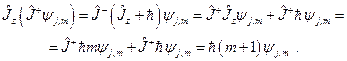
Что и требовалось доказать.

Лемма 2: Если 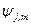- собственный вектор оператора 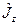с собственным значением 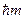, то 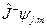тоже есть собственный вектор 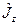с собственным значением 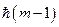, т.е.

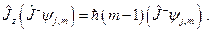
Доказательство проводится аналогично с учетом формул (20.11) и (20.1).

Из рассмотренных вспомогательных лемм в дальнейшем нам понадобятся два следствия:

1) (20.15)

2) 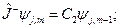(20.16)

где 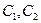- некоторые постоянные.

Данные леммы и их следствия дают ответ на вопрос о спектре собственных значений проекции момента, если нам известно хотя бы одно значение. Согласно леммам 1 и 2 собственные значения проекции момента количества движения 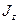, которым принадлежат собственные функции 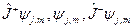, отличаются на единицу и находятся, согласно доказанной теореме, в интервале 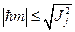. Таким образом, при фиксированном значении 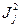значения m ограничены сверху и снизу. Пусть 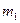и 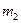соответственно наименьшее и наибольшее значения 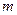при заданном 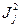, т.е. 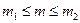. Тогда

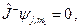(20.17)

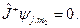(20.18)

С учетом равенств (20.17), (20.14) и (20.18), (20.1) можно записать

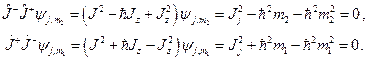
Откуда

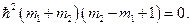
Так как по условию , то , откуда

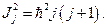(20.19)

Определим значения постоянных 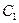и 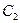в выражениях (20.15), (20.16). Для этого применим условие нормировки

.

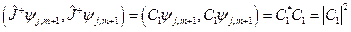С другой стороны,

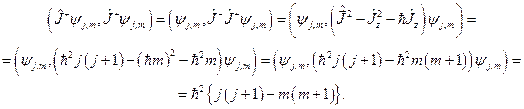
Сравнивая полученные выражения, делаем вывод, что

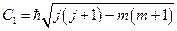, (20.20)

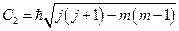. (20.21)

Согласно (20.15), (20.16), (20.20), (20.21):

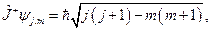(20.22)

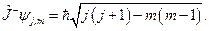(20.23)

Date: 2015-05-18; view: 506; Нарушение авторских прав